The technical aspects of the modeling approach follow the results contained in Berryman (2005), and are summarized in Appendix A. The main idea is based on several facts about polycrystals and the technical issues associated with estimating their properties.
The first and most obvious issue with cracked materials is that, in the vicinity of one crack, the effective elastic properties will necessarily be anisotropic. Since by far the great majority of effective medium and other upscaling methods for composite materials have been designed for overall isotropic composites composed of isotropic constituents, we necessarily must try something rather different for cracked materials. It seems natural to suppose that the cracked medium may be viewed as a collection of randomly oriented grains of various sizes and orientations containing cracks. For the dilute case having rather small crack densities, we could imagine that each grain has only one crack per grain. But, as the crack density increases, cracks may intersect with other cracks. In this case, we may have multiple cracks and/or intersecting cracks in each grain.
The shape of the cracked grains is another possible variable within the model. It is fairly common in the study of polycrystals to assume that the grains are spherical (Olson and Avellaneda, 1992). Since it is clear that it is not possible to fill all of space with spheres of the same size, such a model requires a further assumption that the grains come in a wide variety of sizes down to the infinitesimal and that this happens in a way that does fill all space. It seems clear that this type of model is artificial in the sense that it applies to no real material, but it nevertheless is a model that has been used extensively in effective medium theories and generally seems to produce reasonable modeling results. Nevertheless, we will avoid this approach here and consider instead an alternative wherein we assume that the cracks come in clusters. A cluster might be just one crack, or several cracks in close proximity. Then we assume each cluster is sufficiently separated from the other crack clusters that we can assign a center point to each cluster and then construct Voronoi polyhedra by drawing planes midway between nearest neighbors so that all of space is partitioned without leaving any holes. 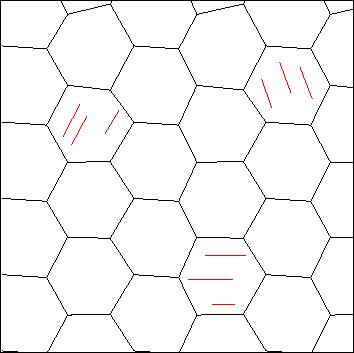Figure 1 illustrates one realization for this model random polycrystal of cracked grains.
|
Fig1
Figure 1 Schematic illustrating the random polycrystals of cracked grains model. Grains are assumed to fit tightly so there is no misfit porosity, although there is some porosity due to the cracks themselves. The shapes of the grains are not necessarily the same, and the symmetry axes of the grains (three examples shown) are randomly oriented so the overall polycrystal is equiaxed (statistically isotropic). |  |
Various rigorous bounds are known for polycrystals [Voigt (1928), Reuss (1929), Hashin-Shtrikman (1962b)], and the commonly used Voigt-Reuss-Hill estimate (arithmetic average of the Voigt and Reuss bounds (Hill, 1952) is both well-known and well-established. It is important to note however that the Hashin-Shtrikman bounds are problematic for the polycrystalline case because it is known that for composites of anisotropic components the Voigt bound is achievable in certain special cases (Milton, 2002). This fact is sufficient to invalidate the use of the Hashin-Shtrikman bounds as a general method (since the upper HS bound is always smaller than the Voigt bound, thus precluding the possibility of achieving the Voigt bound in the cases where this is known to be an exact result - IF the HS upper bound were valid). Thus, HS bounds must be used cautiously, if at all for anisotropic media, and with the understanding that there are various implicit assumptions in the HS theory that may or may not be satisfied in a given composite having anisotropic constituents (Milton, 2002).
On the other hand, there are also general self-consistent estimators available for these same anisotropic composites (Willis, 1977, 1981; Berryman, 2005). These self-consistent estimators actually do lie between the Hashin-Shtrikman bounds, but -- since they are merely estimates of the average behavior and not bounds in any sense -- they do not suffer from the same questions concerning their validity as the HS bounds themselves. These self-consistent estimates for polycrystals have approximately the same theoretical significance as the Voigt-Reuss-Hill estimates, and should therefore provide generally useful quantitative measures of expected average elastic behavior of polycrystals. We use both types of estimates (Voigt-Reuss-Hill and self-consistent) here when we need values of effective bulk and shear moduli: (1) we use the VRH approach as a means of estimating the effective bulk and shear moduli that can be associated with the stiffness matrices generated by the numerical methods and (2) we use the self-consistent estimator as a means of quantifying the average behavior associated with our predictions and/or fitted values for the polycrystal model.
In the following examples, we find that the HS bounds are in fact much too close together to be useful in explaining the range of behavior observed in the numerical data considered here. However, the Voigt and Reuss bounds do give very good estimates for the range in behavior, while the self-consistent estimator gives a good estimate of the average behavior.