




Next: About this document ...
Up: REFERENCES
Previous: Algorithm for Computation
The iterative solution method can be broken down into a number of
distinct steps: i) define initial grid using blending functions in
equation 29; ii) compute functions
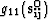 ,
, 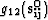 ,
,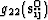 ,
, 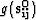 , Lij(u0),
Lij(v0), Mij(u0), Mij(v0),
, Lij(u0),
Lij(v0), Mij(u0), Mij(v0), 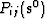 ,
,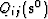 , and
, and 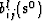 ; iii) compute
uij0+1/2 by solving equation 31; iv) compute
vij0+1/2 by solving equation 32; v) compute
uij0+1 by solving equation 33; vi) compute
vij0+1 by solving equation 34; vii) perform
tolerance test in equation 51; and viii) repeat steps 2-7
until tolerance is reached.
; iii) compute
uij0+1/2 by solving equation 31; iv) compute
vij0+1/2 by solving equation 32; v) compute
uij0+1 by solving equation 33; vi) compute
vij0+1 by solving equation 34; vii) perform
tolerance test in equation 51; and viii) repeat steps 2-7
until tolerance is reached.





Next: About this document ...
Up: REFERENCES
Previous: Algorithm for Computation
Stanford Exploration Project
4/5/2006