Next: Multiple Attenuation
Up: Alvarez: Multiple attenuation
Previous: Theory overview
The better fit of the ray bending approximation to the actual moveout of the multiple,
as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , suggests that a better focusing may be
achieved for the multiples in the Radon domain by using equation 6
as the kernel of the Radon transform. To assess validity of this claim, I used the
same synthetic data presented in Sava and Guitton 2003.
Figure
, suggests that a better focusing may be
achieved for the multiples in the Radon domain by using equation 6
as the kernel of the Radon transform. To assess validity of this claim, I used the
same synthetic data presented in Sava and Guitton 2003.
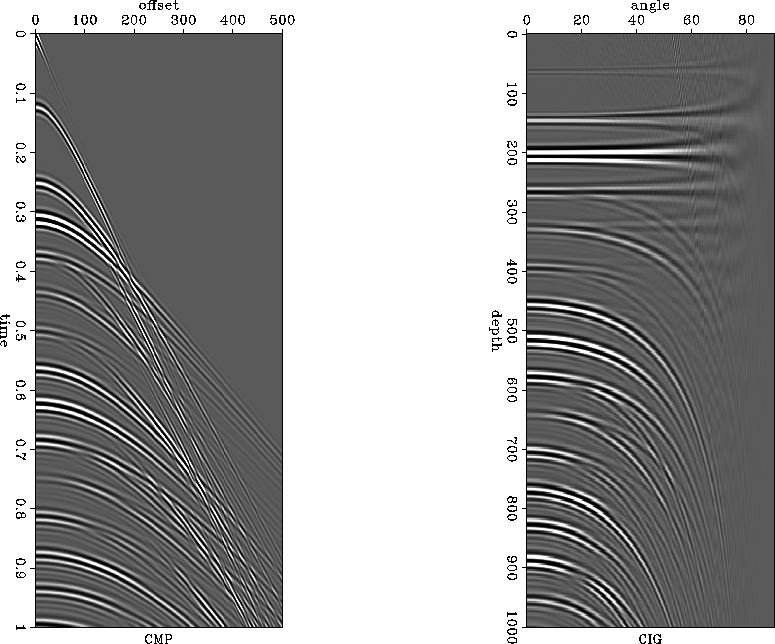
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is their figure 1 and shows a CMP and an ADCIG
contaminated with multiples. Clearly, the primaries are flat in
the ADCIGs (above about 350 m), whereas the multiples show the expected
overmigrated residual moveout.
synth
is their figure 1 and shows a CMP and an ADCIG
contaminated with multiples. Clearly, the primaries are flat in
the ADCIGs (above about 350 m), whereas the multiples show the expected
overmigrated residual moveout.
synth
Figure 3 A data CMP and an ADCIG from a simple synthetic model.
Figure taken from Sava and Guitton 2003.

The general expression for the Radon transform in the angle domain is
Sava and Guitton (2003)
| 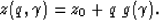 |
(9) |
The straight-ray approximation uses
| 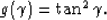 |
(10) |
The ray-bending approximation uses
| ![\begin{displaymath}
g(\gamma)=\frac{1}{1+\rho}\left[\frac{\cos\gamma(\rho^2-(1-\rho^2)\tan^2\gamma)}{\sqrt{\rho^2-\sin^2\gamma}}-\rho\right].\end{displaymath}](img21.gif) |
(11) |
radon1
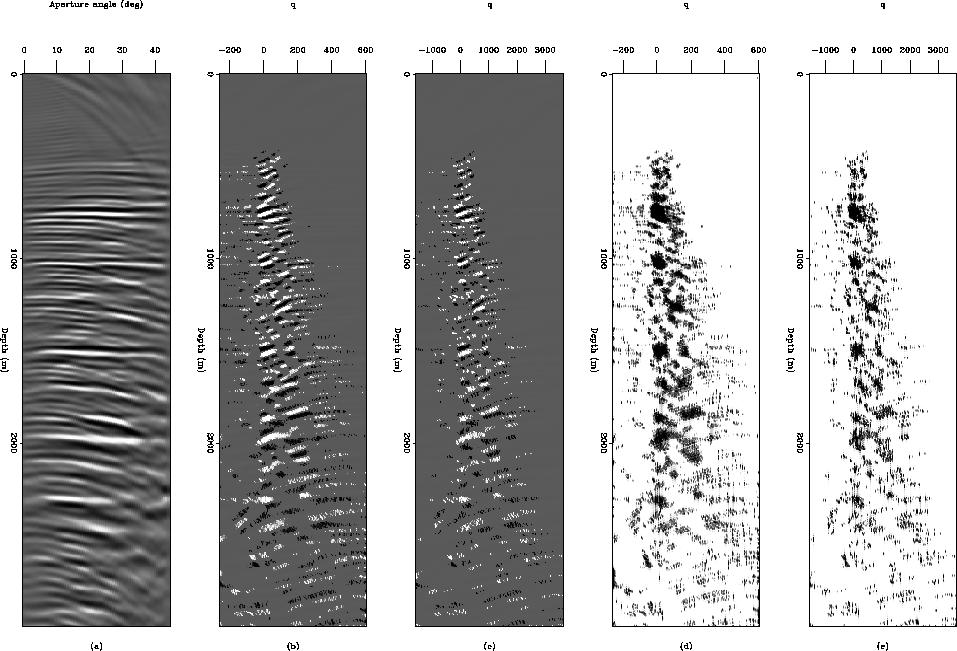
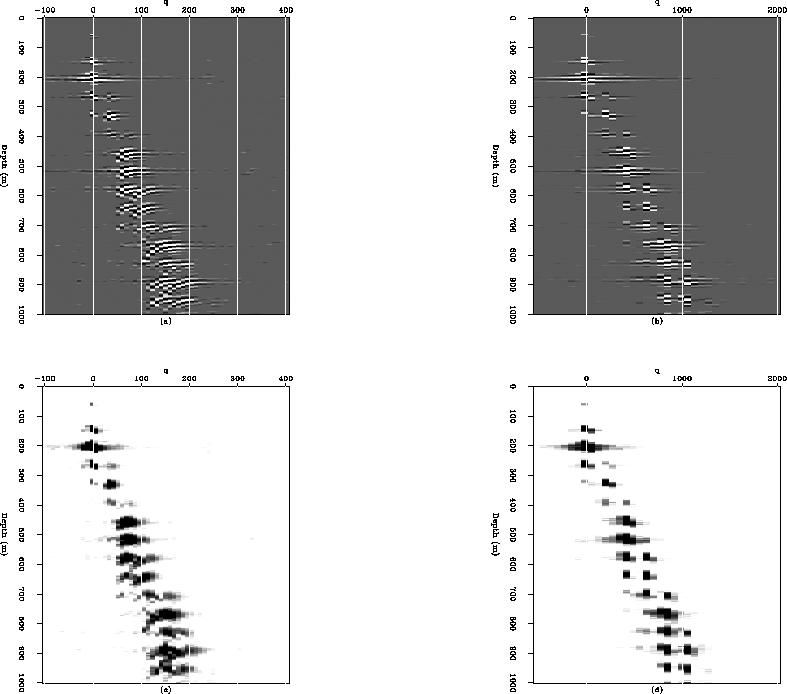
Figure 4 Comparison of Radon transforms of the ADCIG shown in
panel (a) of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Panel (a) corresponds to the straight-ray
approximation
whereas panel (b) corresponds to the ray-bending approximation. Panel (c) and (d)
are the envelopes of panels (a) and (b) respectively.
. Panel (a) corresponds to the straight-ray
approximation
whereas panel (b) corresponds to the ray-bending approximation. Panel (c) and (d)
are the envelopes of panels (a) and (b) respectively.





Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a comparison of both Radon transforms for the ADCIG
shown in the left panel of Figure
shows a comparison of both Radon transforms for the ADCIG
shown in the left panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Notice that the focusing of
the primaries does
not change since their moveout is zero. The multiples, on the other hand, are
better focused with the new transform since the curvature more closely represents
their residual moveout in the ADCIGs.
In order to assess the improvement in focusing power of the new transform with
real data, I applied both Radon transforms to an ADCIG from a real dataset
Sava and Guitton (2003). Figure
. Notice that the focusing of
the primaries does
not change since their moveout is zero. The multiples, on the other hand, are
better focused with the new transform since the curvature more closely represents
their residual moveout in the ADCIGs.
In order to assess the improvement in focusing power of the new transform with
real data, I applied both Radon transforms to an ADCIG from a real dataset
Sava and Guitton (2003). Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ADCIG and
the transforms computed with the straight-ray and the ray-bending approximations.
Again, the ray-bending approximation improves the focusing of the primaries.
This may be better seen in the envelopes of the two transforms.
shows the ADCIG and
the transforms computed with the straight-ray and the ray-bending approximations.
Again, the ray-bending approximation improves the focusing of the primaries.
This may be better seen in the envelopes of the two transforms.
radon2
Figure 5 ADCIG from a real dataset (a), the Radon transform
corresponding to the straight-ray approximation (b), and the Radon transform
with the ray-bending approximation (c). Panels (d) and (e) are the envelopes
of panels (b) and (c).










Next: Multiple Attenuation
Up: Alvarez: Multiple attenuation
Previous: Theory overview
Stanford Exploration Project
4/5/2006
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , suggests that a better focusing may be
achieved for the multiples in the Radon domain by using equation 6
as the kernel of the Radon transform. To assess validity of this claim, I used the
same synthetic data presented in Sava and Guitton 2003.
Figure
, suggests that a better focusing may be
achieved for the multiples in the Radon domain by using equation 6
as the kernel of the Radon transform. To assess validity of this claim, I used the
same synthetic data presented in Sava and Guitton 2003.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is their figure 1 and shows a CMP and an ADCIG
contaminated with multiples. Clearly, the primaries are flat in
the ADCIGs (above about 350 m), whereas the multiples show the expected
overmigrated residual moveout.
is their figure 1 and shows a CMP and an ADCIG
contaminated with multiples. Clearly, the primaries are flat in
the ADCIGs (above about 350 m), whereas the multiples show the expected
overmigrated residual moveout.

![\begin{displaymath}
g(\gamma)=\frac{1}{1+\rho}\left[\frac{\cos\gamma(\rho^2-(1-\rho^2)\tan^2\gamma)}{\sqrt{\rho^2-\sin^2\gamma}}-\rho\right].\end{displaymath}](img21.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Panel (a) corresponds to the straight-ray
approximation
whereas panel (b) corresponds to the ray-bending approximation. Panel (c) and (d)
are the envelopes of panels (a) and (b) respectively.
. Panel (a) corresponds to the straight-ray
approximation
whereas panel (b) corresponds to the ray-bending approximation. Panel (c) and (d)
are the envelopes of panels (a) and (b) respectively.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a comparison of both Radon transforms for the ADCIG
shown in the left panel of Figure
shows a comparison of both Radon transforms for the ADCIG
shown in the left panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Notice that the focusing of
the primaries does
not change since their moveout is zero. The multiples, on the other hand, are
better focused with the new transform since the curvature more closely represents
their residual moveout in the ADCIGs.
In order to assess the improvement in focusing power of the new transform with
real data, I applied both Radon transforms to an ADCIG from a real dataset
Sava and Guitton (2003). Figure
. Notice that the focusing of
the primaries does
not change since their moveout is zero. The multiples, on the other hand, are
better focused with the new transform since the curvature more closely represents
their residual moveout in the ADCIGs.
In order to assess the improvement in focusing power of the new transform with
real data, I applied both Radon transforms to an ADCIG from a real dataset
Sava and Guitton (2003). Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ADCIG and
the transforms computed with the straight-ray and the ray-bending approximations.
Again, the ray-bending approximation improves the focusing of the primaries.
This may be better seen in the envelopes of the two transforms.
shows the ADCIG and
the transforms computed with the straight-ray and the ray-bending approximations.
Again, the ray-bending approximation improves the focusing of the primaries.
This may be better seen in the envelopes of the two transforms.