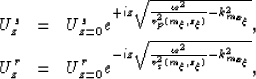Next: Transformation to the angle
Up: Rosales et al.: PS-ADCIG
Previous: Introduction
A prestack image provides information on both velocity errors
and rock-property characteristics. This paper obtains the
prestack image through wave-equation methods. Several authors
have described this process in general, so it will not be
the main focus of this paper. However, this section
describes the basics of wave-equation imaging, and outlines
the method we use to obtain subsurface offset-domain
common-image gathers.
Biondi (2003) shows the equivalence of wave-equation
source-receiver migration with wave-equation shot-profile
migration. The main contribution of this paper is independent
of the migration algorithm implemented, as long as the migration
algorithm is based on the wavefield downward continuation,
and the final prestack image is a function of the horizontal
subsurface offset. For the purposes of this paper,
we are using shot-profile migration as our
imaging algorithm.
The final prestack image is obtained with the following
imaging condition Sava and Fomel (2005):
| 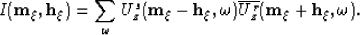 |
(1) |
Here, 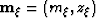 is a vector describing
the locations of the image points, and
is a vector describing
the locations of the image points, and 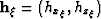 is a vector describing the subsurface
offset. For 2-D converted-wave seismic data, the component
is a vector describing the subsurface
offset. For 2-D converted-wave seismic data, the component 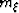 represents the horizontal coordinate,
represents the horizontal coordinate,
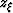 is the depth coordinate of the image point relative to a reference
coordinate system, and
is the depth coordinate of the image point relative to a reference
coordinate system, and 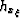 is the horizontal subsurface offset Rickett and Sava (2002).
The summation over temporal
frequencies (
is the horizontal subsurface offset Rickett and Sava (2002).
The summation over temporal
frequencies (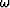 ) extracts the image
) extracts the image 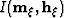 at zero-time.
The propagation of the receiver wavefield (Urz) and the
source wavefield (Usz) is done by
downward continuing the recorded data, and the given source wavelet,
each one respectively as:
at zero-time.
The propagation of the receiver wavefield (Urz) and the
source wavefield (Usz) is done by
downward continuing the recorded data, and the given source wavelet,
each one respectively as:
| 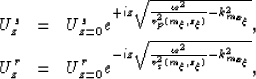 |
|
| (2) |
where vp is the P-wave velocity and
vs is the S-wave velocity.
The next section describes the main focus of this paper,
which is the transformation of subsurface offset into the
angle domain.





Next: Transformation to the angle
Up: Rosales et al.: PS-ADCIG
Previous: Introduction
Stanford Exploration Project
4/5/2006