




Next: Example
Up: R. Clapp: A modified
Previous: Lloyd's Method
Lloyd's method would not lead to an interesting result
for a signal that has a uniform distribution. The
result would be a set of evenly-spaced points that
span the range of the signal. Lloyd's method is effective
for a signal that tends to cluster around a few selected
values (what turns into the codebook).
The velocity selection problem is effectively handled
by the Lloyd approach because the earth is
composed of geologic layers. The velocity range
within a geologic layer tend to be relatively constant.
Lloyd's algorithm automatically identifies these clusters.
In some problems we have several parameters
at every model location. If these parameters
are correlated, a clustering techniques such
as Lloyd's approach can be effective.
Extending the 1-D approach described above
to a 3-D case is relatively simple:
- The codebook entries become vectors rather than scalers.
- To find the nearest point, we do a vector distance calculation.
- Instead of averaging the points attached to a given codebook,
we find the centroid of the attached points.
These changes are all making an assumption that the range of each element
of our vector field is approximately the same. If this assumption isn't true,
for example when our vector field consists of velocity (ranging from 1500-4500 m/s)
and 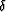 (ranging from 0-.1), we need to scale the
(ranging from 0-.1), we need to scale the 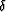 value so
their range is approximately equal to velocity. If we do not, the
value so
their range is approximately equal to velocity. If we do not, the 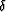 values will have such a small effect in our calculations that the algorithm
reduces to a 1-D velocity solution.
values will have such a small effect in our calculations that the algorithm
reduces to a 1-D velocity solution.





Next: Example
Up: R. Clapp: A modified
Previous: Lloyd's Method
Stanford Exploration Project
4/5/2006