

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: Theory
Up: Table of Contents
AMO inversion to a common azimuth dataset: Field data results
Robert G. Clapp
bob@sep.stanford.eda
ABSTRACT
I cast 3-D data regularization as a least-squares inversion problem.
I form a linear operator
that maps from irregular dataspace 5-D data space to a regular 4-D common
azimuth volume using a cascade of linear interpolation and Azimuth Move-out
(AMO) binning. I regularize the inversion by adding
minimizes the difference between various
(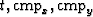 ) cubes by applying
a filter that acts along offset. AMO is used to
transform the cubes to the same hx before applying
the filter.
Further efficiency is gained by inverting each frequency independently.
I apply the methodology on marine dataset and compare
the results with two more conventional approaches. ) cubes by applying
a filter that acts along offset. AMO is used to
transform the cubes to the same hx before applying
the filter.
Further efficiency is gained by inverting each frequency independently.
I apply the methodology on marine dataset and compare
the results with two more conventional approaches.
|
The irregularity of seismic data, particularly 3-D data, in both
the model domain (in terms of subsurface position and reflection angle)
and the data domain (in terms of midpoint, offset, and time) causes
imaging problems.
Migration methods desire a greater level of regularity
than is often present in seismic surveys.
There are two general approaches to deal with this
problem. One approach is to treat the imaging problem
as an inverse problem.
The migration operator can be thought of as a linear transform from
the recorded data to image space.
Duquet and Marfurt (1999); Prucha et al. (2000); Ronen and Liner (2000) use the migration operator
in a linear inverse problem to overcome irregular and limited
data coverage. A regularization that encourages consistency over reflection
angle is used to stabilize the inverse.
These approaches have shown promise but are generally
prohibitively expensive, and rely on an accurate subsurface velocity model.
Another approach is to try to regularize the data.
AMO provides an effective
regularization tool Biondi et al. (1998)
and is generally applied as an adjoint
to create a more regularized volume.
These regularized volumes still
often contain an `acquisition footprint' or more
subtle amplitude effects.
Chemingui (1999) used
a log-stretch transform to make the AMO operator
stationary in time. He then cast the regularization
problem as a frequency-by-frequency inversion problem
using a Kirchoff-style AMO operator.
He showed that the acquisition footprint could be significantly
reduced.
The downside of this approach is the relatively high
cost of Kirchoff implementation of AMO.
Biondi and Vlad (2001) built on the work of
Fomel (2001)
and set up an inverse problem relating the
irregular input data to a regular model space.
They regularized the problem by enforcing consistency between the various
(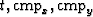 ) cubes. The consistency took two forms.
In the first, a simple difference between two adjacent in-line offset cubes was minimized.
In the second, the difference was taken after transforming the cubes
to the same offset AMO.
Clapp (2005b) set up the data regularization with AMO
as an inverse problem creating a full volume (
) cubes. The consistency took two forms.
In the first, a simple difference between two adjacent in-line offset cubes was minimized.
In the second, the difference was taken after transforming the cubes
to the same offset AMO.
Clapp (2005b) set up the data regularization with AMO
as an inverse problem creating a full volume (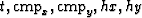 ).
Clapp (2005a) modified this approach to form a Common Azimuth
dataset. The full volume of Clapp (2005b) is mapped
into a Common Azimuth volume using AMO as part of the inversion.
).
Clapp (2005a) modified this approach to form a Common Azimuth
dataset. The full volume of Clapp (2005b) is mapped
into a Common Azimuth volume using AMO as part of the inversion.
In this paper, I build on the work of Clapp (2005a).
I modify the data mapping operator to allow more mingling between
hx volumes in the model space. In addition, each log-stretched frequency
is done independently, allowing many more iterations to be applied economically.
The methodology is applied on a marine dataset and compared to both
a flex-binning and more standard AMO based approach.


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: Theory
Up: Table of Contents
Stanford Exploration Project
4/5/2006
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)