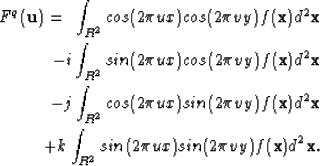Next: Quaternionic Gabor Filters
Up: Hypercomplex Mathematics
Previous: Hypercomplex Mathematics
Analogous to complex numbers, quaternions can be represented by
a magnitude and three phases with
| 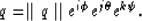 |
(10) |
Ell (1992) introduced the quaternionic Fourier transform (QFT) for
two-dimensional signals,
| 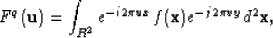 |
(11) |
where 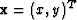 and
and 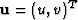
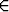 R2 and
f is a two-dimensional quaternion signal. Because
two-dimensional signals can be decomposed into even and odd components along
either the x- or y-axis, f can be written
with, for example, foe denoting the part of f that is odd with respect to
x and even with respect to y. The QFT can now be decomposed to
R2 and
f is a two-dimensional quaternion signal. Because
two-dimensional signals can be decomposed into even and odd components along
either the x- or y-axis, f can be written
with, for example, foe denoting the part of f that is odd with respect to
x and even with respect to y. The QFT can now be decomposed to
| 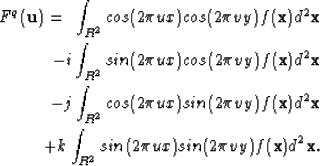 |
|
| |
| |
| (12) |
The QFT is an invertible transform and most
standard Fourier theorems hold for QFTs with minimal variation.
These theorems will not be rederived here, as
complete proofs of the QFT extension of Rayleigh's, the shift,
the modulation, the derivative, and the convolution theorem exist
elsewhere Bülow (1999); Ell (1992).





Next: Quaternionic Gabor Filters
Up: Hypercomplex Mathematics
Previous: Hypercomplex Mathematics
Stanford Exploration Project
4/5/2006