Principles of focusing

Figure 1 geometrically shows the depth-focusing process of the primary scattered wavefield, and Figure 2 shows the same process for the multiple scattered wavefield. Comparing the two figures, it is clearly seen that the focusing process is the same for a scattering point, whether the scattered wavefield from it is primary or multiple scattering.

 

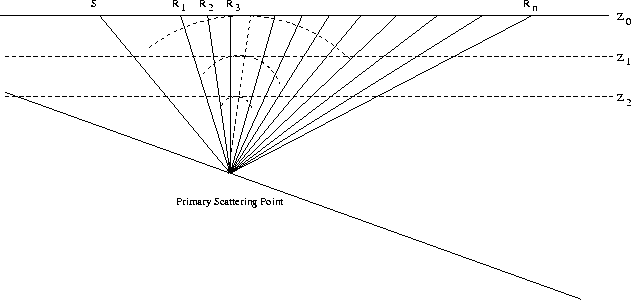Scattering_primary Figure 1 The depth focusing of the primary scattering wavefield with the extrapolation. The radius of curvature of the wavefront diminishes to zero with the downward wavefield continuation.

 

Scattering_multiples Figure 2 The depth focusing of the multiple scattering wavefield with the extrapolation. The source position can be unknown. The radius of curvature of the wavefront diminishes into zero with the downward wavefield continuation. The higher-order multiples can be focused also.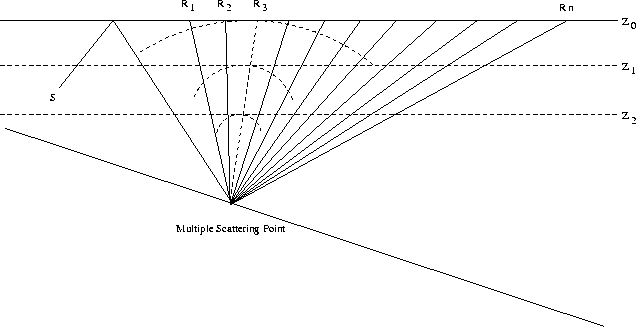

The imaging condition of prestack migration is that the arrival time of the downgoing wave equals the take-off time of the upcoming wave Claerbout (1971). However, conventionally, the downgoing wave means the primary downgoing wave, not the multiple downgoing wave. It is difficult to determine the traveltime of the multiple downgoing wave. Therefore, with this imaging condition, it is difficult to image the primaries and the multiples simultaneously. The conventional imaging condition implicitly tell us that the image of a reflector appears at the point, at which the received scattered wavefield is collapsed. At that point, the arrival time of the downgoing wave equals the take-off time of the upcoming wave, and the radius of curvature of the scattered wavefield diminishes to zero. The radius of curvature of the scattered wavefield diminishes to zero means that the scattered wavefield is focused to the scattering point. Unlike imaging for the primaries, for imaging of multiples, the concept of offset makes no sense. For multiples imaging, the offset should be calculated with the "pseudo" source and receiver position. However, it is not easy to determine the "pseudo" source position for the higher-order multiples. In fact, the statement that the arrival time of the downgoing wave equals the take-off time of the upcoming wave is equivalent to saying that the radius of curvature of the scattering wavefield diminishes to zero. However, the latter is much more prevalent than the former. The latter can be used to image the primaries and the multiples, whether the source position is known or unknown, because the only criterion is whether the scattering wavefield is focused or not. The latter can be called the depth-focusing imaging condition. The former is a model-driven process; the latter is a hybrid-driven process. Wavefield extrapolation is model-driven, and picking the focused amplitude is data-driven.