Next: (C) Non-linear waveform inversion
Up: comparison among migration/inversion methods
Previous: (3) Least-squares migration/inversion
We can define a minimizing problem that aims at finding 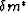 by minimizing the following cost function:
by minimizing the following cost function:
| 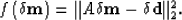 |
(47) |
The Newton iterative algorithms can be used for solving the minimizing problem. The standard Newton iterative algorithm is
| ![\begin{displaymath}
\delta \textbf{m}^{\left( k+1\right) }=\delta \textbf{m}^{\l...
...ight)\right]^{-1} \nabla f\left(\delta \textbf{m}^{(k)}\right).\end{displaymath}](img58.gif) |
(48) |
However, the inverse of the Hessian is difficult to calculate. The Quasi-Newton algorithms are used commonly. The inverse of the Hessian matrix can be calculated with the DFP formula:
| 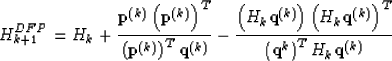 |
(49) |
where 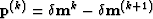 , and
, and 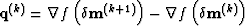 .
.
The Quasi-Newton iterative algorithm is
| 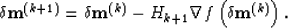 |
(50) |





Next: (C) Non-linear waveform inversion
Up: comparison among migration/inversion methods
Previous: (3) Least-squares migration/inversion
Stanford Exploration Project
11/1/2005