Next: FEAVA removal
Up: Vlad: Focusing-effect AVA
Previous: FEAVO migration and modeling
In order to remove FEAVO/FEAVA, or at least not to trust the
amplitudes from the affected areas, one must be alerted to its
existence. Visual inspection of zero-offset data for subvertical
streaks of high energy provides a cue only in the case of the most
powerful effects. ``Kjartansson V's'' would provide a good diagnostic
tool if it were not for today's prestack data volumes which size in the
terrabytes. Comparing stacks of near and far offsets is a good way of
alerting that something is wrong Hatchell (2000a), but it does not highlight FEAVO specifically. Laurain et al. (2004) give a good way of
quantitatively estimating the amplitudes due solely to propagation
effects for a single reflector at a time. This method is even more
labor-intensive than visually examining the prestack lines for
``V''s. The worst one is to rely on the interpreter to realize if
``something is wrong with the AVO'' - he may just interpolate an
intercept and gradient through the erratic values.
What is needed is a quick, simple and robust way to signal the
corruption of AVO by focusing.
Vlad (2004b) provides such a FEAVA detection
method. The method is based on the fact that reflector-caused AVA for
incidence angles 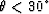 is very well described
Shuey (1985) by
is very well described
Shuey (1985) by
| 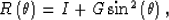 |
(3) |
where I and G depend only on the lithology at the reflector. If
the amplitudes are picked at a single midpoint-depth location not
affected by focusing and plotted as a function of the  ,the values will arrange close to a line with intercept I and
gradient G. The presence of FEAVO causes the linear dependence to
break, as exemplified on a simple synthetic in Figure
,the values will arrange close to a line with intercept I and
gradient G. The presence of FEAVO causes the linear dependence to
break, as exemplified on a simple synthetic in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
examine_FEAVO
.
examine_FEAVO
Figure 10 Top panel:
Midpoint-angle depth slice from the prestack migrated synthetic
dataset shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . From Vlad et al. (2003a).
Bottom panels: Amplitudes at midpoints marked by vertical thin
lines in the upper panel. From
Vlad (2004b).
. From Vlad et al. (2003a).
Bottom panels: Amplitudes at midpoints marked by vertical thin
lines in the upper panel. From
Vlad (2004b).





A direct estimate of the amount of FEAVA energy present at a
(midpoint, depth) location can be obtained by measuring how much
nonlinearity is in the dependence between amplitudes and
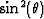 . Simply interpolating a linear trend, subtracting it
and computing the variance of the residual (Figure
. Simply interpolating a linear trend, subtracting it
and computing the variance of the residual (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
provides a computationally cheap procedure with no knobs to turn.
)
provides a computationally cheap procedure with no knobs to turn.
 The
``FEAVO attribute'' output by this detector is ``poststack-sized'',
having no offset dimensions and no intensive human labor requirement
for the visual examination. The vertical clustering of the affected
areas in clusters under the source anomalies helps with the detection
and possibly with the interpretation of the heterogeneities that cause
FEAVA as well. Figure
The
``FEAVO attribute'' output by this detector is ``poststack-sized'',
having no offset dimensions and no intensive human labor requirement
for the visual examination. The vertical clustering of the affected
areas in clusters under the source anomalies helps with the detection
and possibly with the interpretation of the heterogeneities that cause
FEAVA as well. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a simple example obtained
by migrating with the background velocity the synthetic dataset from
Figure
shows a simple example obtained
by migrating with the background velocity the synthetic dataset from
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
anoloc
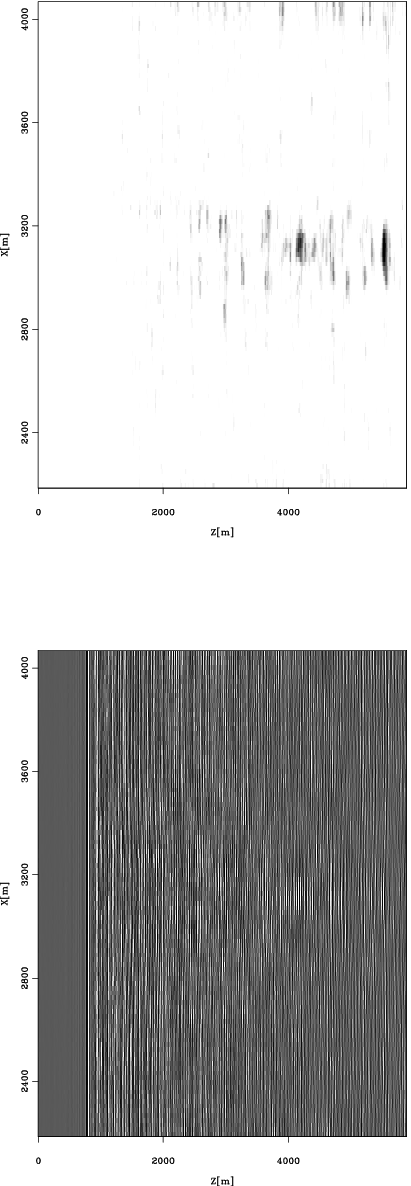
Figure 12 FEAVO
anomalies flagged in the midpoint-depth space by the automatic
detection procedure. The stars denote the location of the
heterogeneities causing the focusing. From Vlad (2004b).
|
|  |




 The FEAVO effects are very visible - everything
that is certainly not FEAVO has been eliminated. By contrast, when
looking for vertical streaks or Kjartansson ``V''s in the data without
the help of the detector, the eye is distracted by the very large
amount of amplitudes that cannot possibly be FEAVO, but are still in
the picture. Figure
The FEAVO effects are very visible - everything
that is certainly not FEAVO has been eliminated. By contrast, when
looking for vertical streaks or Kjartansson ``V''s in the data without
the help of the detector, the eye is distracted by the very large
amount of amplitudes that cannot possibly be FEAVO, but are still in
the picture. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows that the FEAVO
detector functions well in a complex case, with subtle (2-3%
variation from the background) velocity ``lenses'' which produce
barely visible subvertical high amplitude streaks in the
stack.
shows that the FEAVO
detector functions well in a complex case, with subtle (2-3%
variation from the background) velocity ``lenses'' which produce
barely visible subvertical high amplitude streaks in the
stack.
com_nomult_imag
Figure 13 The FEAVO detector performs
well on realistic data. Notice how barely visible focusing in the
stack (top panel) is amplified by the detector (bottom panel). The
erratic values in the upper part of the detector output are from
above the sea bottom. From Vlad (2004a).
|
|  |





The robustness of the FEAVO detector is confirmed by its behavior in
the presence of multiples. In Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) multiples are also weakly highlighted, but they are not vertically
correlated like FEAVO and therefore they are not a serious source of noise.
multiples are also weakly highlighted, but they are not vertically
correlated like FEAVO and therefore they are not a serious source of noise.
The output of the detector could be improved in principle by
subtracting an interpretation-based estimation of the lithology-caused
AVO, instead of just the best fitting line. However, this would
introduce complexity, expense and sources of errors for marginal
gains. Simple as it is, the FEAVO detector works well independently
for each midpoint, even when the rock-caused AVO is unknown, and even
in the presence of multiples or limited aperture angles
Vlad (2004a). A significant increase in complexity
appears to be necessary, however, when trying to remove FEAVO from the
data, which is the subject of the next section.
bg-refvel1top2
Figure 14 Left:
V(z) migration of FEAVO-affected data with internal multiples. The
streak of energy in the center is barely visible. Right:
Applying the FEAVO detector really highlights the focusing
effects. From Vlad (2004a).










Next: FEAVA removal
Up: Vlad: Focusing-effect AVA
Previous: FEAVO migration and modeling
Stanford Exploration Project
5/3/2005
![]() is very well described
Shuey (1985) by
is very well described
Shuey (1985) by
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . From Vlad et al. (2003a).
Bottom panels: Amplitudes at midpoints marked by vertical thin
lines in the upper panel. From
Vlad (2004b).
. From Vlad et al. (2003a).
Bottom panels: Amplitudes at midpoints marked by vertical thin
lines in the upper panel. From
Vlad (2004b).
![]() . Simply interpolating a linear trend, subtracting it
and computing the variance of the residual (Figure
. Simply interpolating a linear trend, subtracting it
and computing the variance of the residual (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
provides a computationally cheap procedure with no knobs to turn.
)
provides a computationally cheap procedure with no knobs to turn. 
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a simple example obtained
by migrating with the background velocity the synthetic dataset from
Figure
shows a simple example obtained
by migrating with the background velocity the synthetic dataset from
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
. 
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows that the FEAVO
detector functions well in a complex case, with subtle (2-3%
variation from the background) velocity ``lenses'' which produce
barely visible subvertical high amplitude streaks in the
stack.
shows that the FEAVO
detector functions well in a complex case, with subtle (2-3%
variation from the background) velocity ``lenses'' which produce
barely visible subvertical high amplitude streaks in the
stack.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) multiples are also weakly highlighted, but they are not vertically
correlated like FEAVO and therefore they are not a serious source of noise.
multiples are also weakly highlighted, but they are not vertically
correlated like FEAVO and therefore they are not a serious source of noise.