| |
(2) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) plots this surface.
plots this surface.
|
feavo_imag
Figure 6 FEAVO path in ADCIGs, constant velocity, flat reflectors, heterogeneity 20m deep. Unlike in the data domain, the shape keeps on opening with depth and the arms of the ``V's'' are slightly curved. | 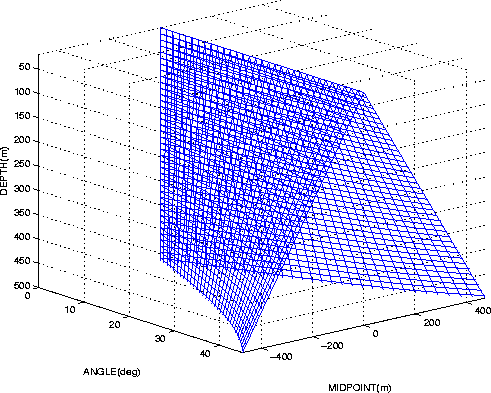 |
The ``Kjartansson V's'' are visible in the Grand Isle dataset after a
v(z) survey-sinking migration. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows two
depth slices through the prestack image. The number of ``V''s is
particularly large in this dataset, making it less than suitable for
isolating and studying a FEAVO instantiation free from
interference. In a less crowded area of the figure, the circled
upside-down ``V'' shows vertical continuity as well as borders of
polarity opposite from that of the main image, as predicted by
finite-frequency wave theory Spetzler et al. (2004). Another
property of data-domain FEAVO that gets carried over in the image
domain is the dependence of the polarity of the effects on the sign of
the velocity ``lenses'' (Figure
shows two
depth slices through the prestack image. The number of ``V''s is
particularly large in this dataset, making it less than suitable for
isolating and studying a FEAVO instantiation free from
interference. In a less crowded area of the figure, the circled
upside-down ``V'' shows vertical continuity as well as borders of
polarity opposite from that of the main image, as predicted by
finite-frequency wave theory Spetzler et al. (2004). Another
property of data-domain FEAVO that gets carried over in the image
domain is the dependence of the polarity of the effects on the sign of
the velocity ``lenses'' (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The effects along
the described paths have a finite width, as exemplified by Figure
). The effects along
the described paths have a finite width, as exemplified by Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . In the case of velocity-caused FEAVO, the width of
the path is linked to both the magnitude and the size of the
heterogeneity. It is not known to what extent there is a
magnitude-size ambiguity in the case of absorption. For both cases it
may be possible to put an upper bound on the spatial extent of the
anomaly based on the width of the FEAVO path, and this can be used as
regularization in inversion for the anomalies or as an aid in
interpretation.
. In the case of velocity-caused FEAVO, the width of
the path is linked to both the magnitude and the size of the
heterogeneity. It is not known to what extent there is a
magnitude-size ambiguity in the case of absorption. For both cases it
may be possible to put an upper bound on the spatial extent of the
anomaly based on the width of the FEAVO path, and this can be used as
regularization in inversion for the anomalies or as an aid in
interpretation.
| Needed: A study of the link between the magnitude (intensity) and size (spatial extent) of the FEAVO source and the width of the FEAVA effects. This applies to data-domain effects too. |
Migration removes any focusing effects which did not send energy
outside the survey aperture Vlad (2005), so it will be
easier to study FEAVA effects in the image than in the data - there
is simply much less misplaced energy to interfere with the object of
study.![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) To
properly view (and extract) FEAVA, one must first resolve the background
velocity well enough that there is no residual first-order curvature
in ADCIGs. FEAVA effects, being caused by anomalies much smaller than the
cable length, will manifest themselves as slight traveltime wiggling
accompanied by high/low amplitudes. Figure
To
properly view (and extract) FEAVA, one must first resolve the background
velocity well enough that there is no residual first-order curvature
in ADCIGs. FEAVA effects, being caused by anomalies much smaller than the
cable length, will manifest themselves as slight traveltime wiggling
accompanied by high/low amplitudes. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a synthetic
example obtained of FEAVA effects ``in a pure state'', after all
non-FEAVA energy has been removed.
shows a synthetic
example obtained of FEAVA effects ``in a pure state'', after all
non-FEAVA energy has been removed.
The advantage of having less clutter in the image can be easily negated by a treatment of the data that emphasizes lack of noise over amplitude preservation. A comparation of Figure 2 in Vlad (2002) and Figure 6 in Vlad and Biondi (2002) shows an example of such an occurence. Using an amplitude-preserving processing and imaging flow is critical for correctly imaging the effects. Smearing the FEAVO effects with amplitude-careless processing is not removing them, but sweeping the dirt under the rug, since this will result in undesired FEAVO energy contaminating now unknown areas. Also, FEAVO removal may need to take into account the physics of the phenomenon, which need to be preserved. Vlad et al. (2003b) and Vlad and Tisserant (2004) describe the implementation of an amplitude-preserving shot-profile migration. The processing done before migration needs to use amplitude-preserving algorithms too.
|
Needed: A study of the amplitude properties of the
offset-to-angle transformation used in creating the ADCIGs, and in
particular the role of the regularization |
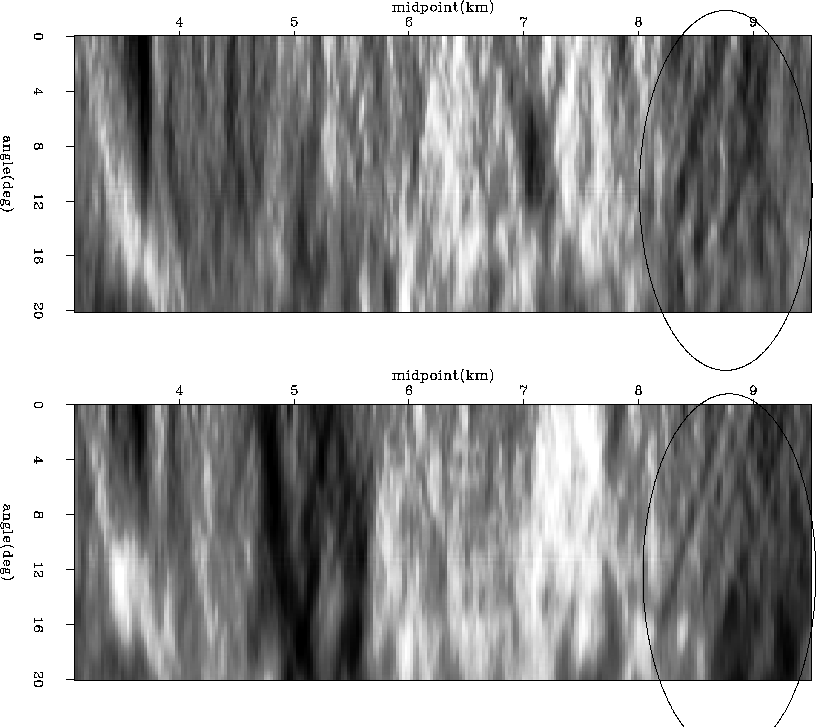 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ; (2)
its opposite-polarity borders; and
(3) the rectangular shaded areas spanning all angles which may denote
``legitimate'', reflector-caused AVO if reflectors are flat enough
in this area.
; (2)
its opposite-polarity borders; and
(3) the rectangular shaded areas spanning all angles which may denote
``legitimate'', reflector-caused AVO if reflectors are flat enough
in this area.
An important point to note is that there is no relationship
whatsoever between amplitude variations caused by focusing and those
caused by variation of incidence angle on the reflector
(FEAVO vs. ``legitimate'' AVO). The total amplitude of a reflector
will show a superposition of the two effects, but the effects are
physically independent from each other. FEAVO effects do not obey the
sin2 dependence between amplitude and reflection angle given by
Shuey (1985). Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) offers an
illustration of this property, and the ``FEAVO detection'' and ``FEAVO
removal'' sections explore its the applications.
offers an
illustration of this property, and the ``FEAVO detection'' and ``FEAVO
removal'' sections explore its the applications.