Numerical Examples

In this section, we present numerical tests of the theory developed above. We provide the proof-of-concept using a plane-wave teleseismic data set Shragge (2003). This data set is comprised of elastic wavefields, which allows us to test both the diffracted and converted scattering scenarios. The idealized model, shown in Figure , is comprised of three materials with differing elastic properties.

 

Vel
Figure 3 Smoothed version of structural model used in test.

A low-velocity crustal layer (white) overlies a faster upper mantle (dark gray). At the location of the suture, crustal material from the lithospheric block to the left bifurcates, with the lower segment descending into the mantle. At the depth of approximately 40 km, the relict (black) converts to velocities and density higher than the surrounding mantle (with a proportionally greater increase in shear-wave velocity) and thereafter folds and thins to the right of the model. Structural dips in the model are generally quite low (i.e., less than 20); however, sub-vertical discontinuities are present in the zone of short-wavelength structure between x=120 and x=160.

Several sets of two-component seismograms were computed through this model using a 2-D, elastic pseudo-spectral finite-difference code Kosloff et al. (1990). The seismograms comprise a suite of plane P-wave sources interacting with the model over a range of incident horizontal slownesses, $p_s=[\pm 0.05, \pm 0.06, \pm 0.07]$skm^-1. We rotated the output data from the computational orientation (i.e., ${\bf U}=[U_1,U_3]$) to a wave-vector orientation (i.e., ${\bf w}=[P,SV]$) via the free-surface transfer matrix Kennett (1991).

Figure  presents examples of P-wave (top panels) and S-wave (bottom panels) data sections. The left and right panels show data for plane-wave sources incident from the left and right sides of the model in Figure , respectively.

 

data
Figure 4 Examples of plane-wave data used in migration and ADCIG test. a) left-incident P-wave; b) right-incident P-wave; c) left-incident S-wave; and d) right-incident S-wave.

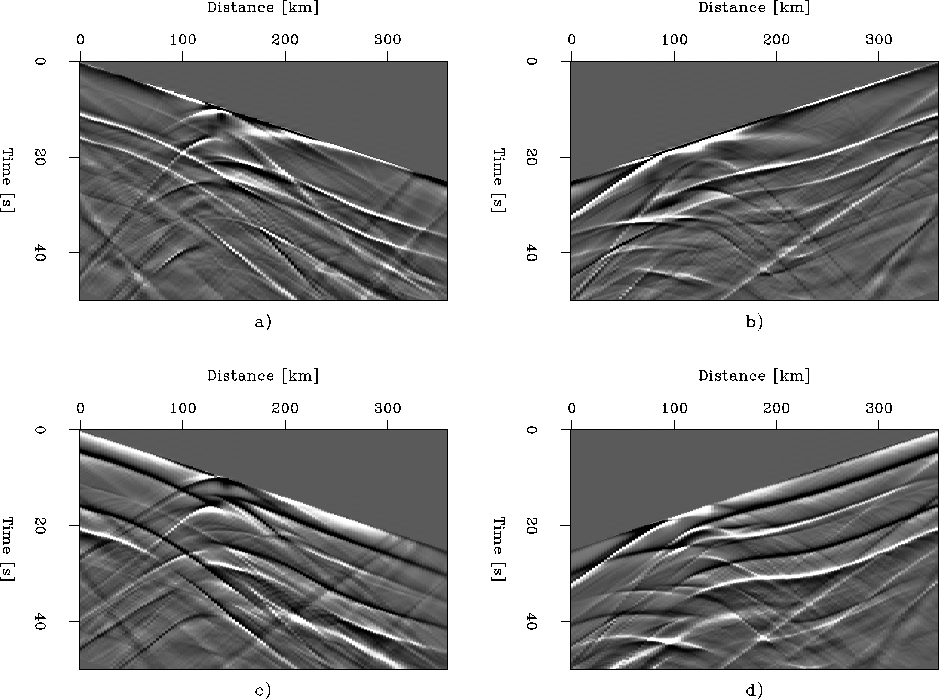We are interested in imaging are the P-P diffracted waves from the zone of short wavelength structure immediately following the plane-wave arrival, and the P-S diffracted and converted waves arriving shortly thereafter.

This vector-wavefield processing yields P- and S-wave data sections appropriate for use in shot-profile migration Shragge et al. (2005). We migrated the data sections for both P-P and P-S scattering modes. We present the image volumes in Figures  and , where horizontal and vertical ADCIGs are shown in the upper and lower panels, respectively. The upper panel of Figure  shows a vertical streak around 130 km in midpoint. This indicates that because of the low geologic dip angles in this model, horizontal ADCIGs computed from forward-scattered P-P migrations afford low resolution of the imaged structure, and are not likely to be useful either for MVA or imaging.

 

Q1
Figure 5 ADCIGs for forward-scattered P-P diffracted wavefields. a) slice through horizontal ADCIG volume at angle 150; b) slice through horizontal ADCIG volume at x=126 km; c) slice through vertical ADCIG at angle 110; and d) slice through vertical ADCIG at x=126 km. Note that the vertical ADCIGs has a slightly better spatial localization of energy.

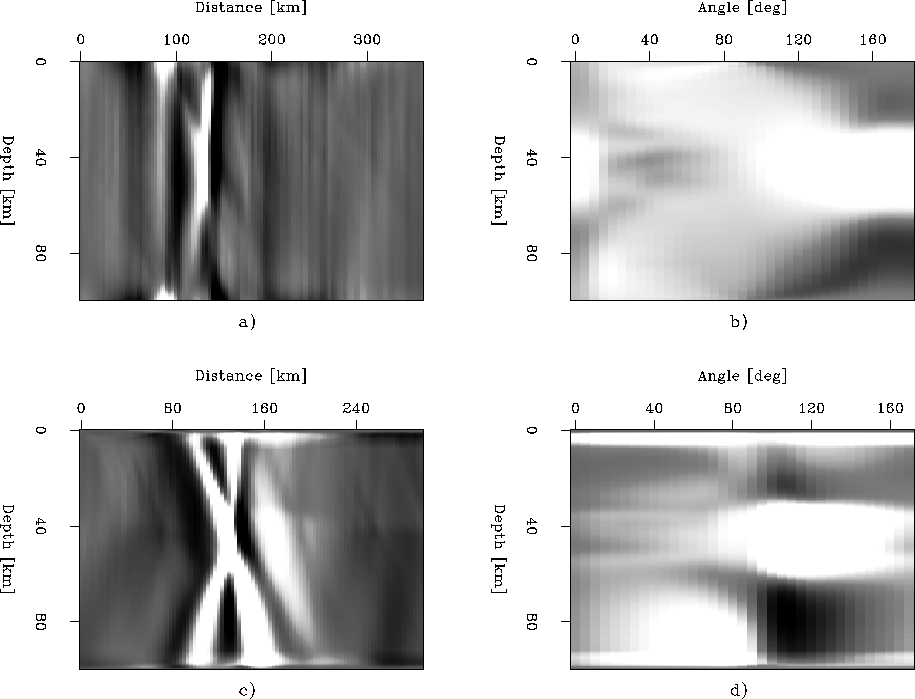In addition, we computed vertical ADCIGs using the method described in the above section (i.e., by replacing horizontal variables x and h_x with vertical variables z and h_z). The vertical ADCIG shown in the lower panels have a slightly better spatial localization of energy. Note that migrated energy in panel d) focuses about 90, which is the forward-scattered equivalent of a zero-offset reflection. Also imaged is a cross-hair pattern about the target zone in panel c) that is directly analogous to smearing commonly observed in tomographic images that derives from limited ray coverage.

The migration results for forward-scattered P-S conversions are shown in Figure . However, we have not yet fully implemented Equation (19), and use Equation (21) as a proxy instead. This is not too grievous of an approximation, as shown by Rosales and Biondi (2005). Hence, angles are not exactly in the correct position. Future work will implement the appropriate expressions. The upper panels show the P-S horizontal ADCIG. Panel b) exhibits clusters of energy on both sides of the 90 mark. These represent groups of 3 plane-waves impinging from the right and left sides of the model that are mapped to different sides of the 90 normal axis. Relative to the equivalent panels in Figure , the forward-scattered horizontal ADCIG indicates that forward-scattered converted waves afford significantly higher resolution than P-P diffractions. This observation is a consequence of the direct link between increased differential arrival times and improved spatial resolution.

 

Q2
Figure 6 ADCIGs for forward-scattered P-S converted wavefields. a) slice through horizontal ADCIG volume at angle 55; b) slice through horizontal ADCIG volume at x=174 km; c) slice through vertical ADCIG at angle 90; and d) slice through vertical ADCIG at x=138 km.

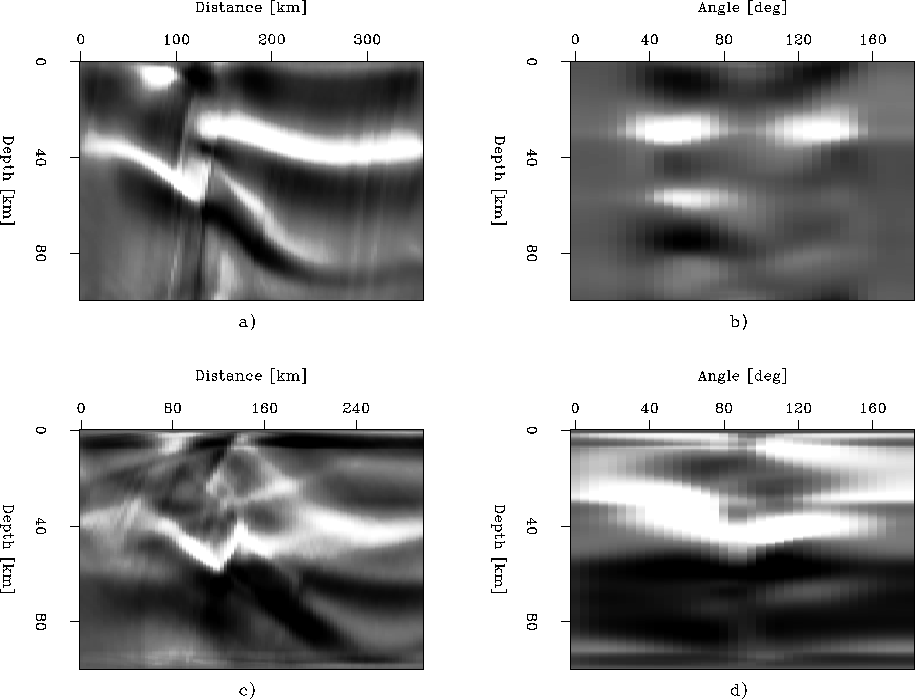The vertical ADCIG volume, shown in the lower panels, again affords better resolution of sub-vertical structure than sub-horizontal interfaces. The zone of short-wavelength structure is better imaged than its counterpart in Figure , and has better angle-domain localization.