From ODCIGs to ADCIGs

An ODCIG can be transformed to another image-space volume, termed an angle-domain common-image gather (ADCIG), representing reflectivity as a function of reflection angle. Sava and Fomel (2003b) present a post-imaging, Fourier-domain transform between these spaces appropriate for conventional reflection wavefields. However, as discussed by Rosales and Rickett (2001), this transform does not hold for converted waves because Snell's Law partitions the total reflection angle into unequal source- and receiver-side reflection contributions.

Figure  illustrates the generalized geometry of the forward-scattering scenario for a subsurface geologic discontinuity, $\overbar{{\bf I}}$, oriented at geologic dip angle, $\alpha$, with normal, $\overbar{{\bf n}}$. An upgoing planar source wavefield propagating at angle $\beta_s$ to the upward vertical has already interacted at $\overbar{{\bf I}}$ to generate an upgoing, planar wavefield propagating at angle $\beta_r$.

 

cig-simple-v4
Figure 2 Sketch denoting the forward-scattered converted wave scenario. An upgoing planar source wavefield propagating at angle $\beta_s$ has already interacted with surface $\overbar{{\bf I}}$ to generate an upgoing planar scattered wavefield, R, propagating at angle $\beta_r$. The total reflection angle, $2\gamma$, is partitioned into source- and receiver-side reflection angles, $\gamma_s$ and $\gamma_r$, according to Snell's Law. Arrows are included on angles to show the sense of rotation, where (counter)clockwise angles are taken here to be (negative) positive quantities.

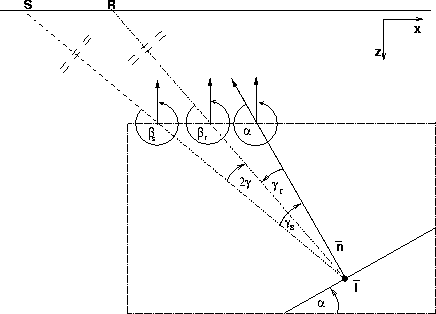For P-P interactions, Snell's Law requires that total reflection opening angle, $2\gamma$, is split equally between the source- and receiver-side reflection angles (i.e., $\gamma=\gamma_r=\gamma_s$). For P-S conversions, Snell's Law requires that angle $2\gamma$ is not bisected into equal components, leaving $\gamma_s$ unequal to $\gamma_r$. Hence, additional constraint equations must be included to isolate the receiver-side reflectivity contributions.

 

• Generating Constraint Equations