




Next: Generating Potential Functions
Up: Theory
Previous: Theory
The scalar form of Laplace's equation is the partial differential
equation,
| 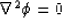 |
(1) |
where 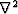 is the second-order spatial derivative operator, and
is the second-order spatial derivative operator, and
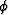 is the sought PF. Laplace's equation is a special case of the
Helmholtz differential equation,
is the sought PF. Laplace's equation is a special case of the
Helmholtz differential equation,
| 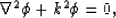 |
(2) |
when wavenumber k=0. A physical interpretation of this observation
is that PF 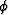 is the zero-frequency solution of the frequency-domain
wave-equation, and is independent of the velocity field and thereby
solely a geometric construct. A harmonic PF satisfying Laplace's
equation has a number of important properties that are
valid either on the boundary of, or entirely within, the defining
domain. Most relevant to this discussion are that a PF:
is the zero-frequency solution of the frequency-domain
wave-equation, and is independent of the velocity field and thereby
solely a geometric construct. A harmonic PF satisfying Laplace's
equation has a number of important properties that are
valid either on the boundary of, or entirely within, the defining
domain. Most relevant to this discussion are that a PF:
- is uniquely determined by either the values,
or normal derivatives thereof, on the domain boundary;
- has an average value over a spherical neighborhood equal to the
value at its center; hence, PFs do not have local maxima or
minima in the domain;
- is curl-free (i.e.,
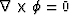 ) ensuring
non-overlapping, and at most simply connected, equipotential surfaces;
) ensuring
non-overlapping, and at most simply connected, equipotential surfaces;
- gradient field is uniquely defined, locally orthogonal to the
equipotential surfaces, and related to the PF through,
| 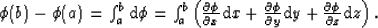 |
(3) |
Each of these properties make PF solutions of Laplace's equation an
important tool for generating orthogonal coordinate systems.





Next: Generating Potential Functions
Up: Theory
Previous: Theory
Stanford Exploration Project
5/3/2005