We test a 2D example to check how the length of a filter affects its accuracy.
The medium is homogeneous, in which the P-wave velocity in the direction parallel to the symmetry axis is 2000m/s,
![]() ,
, ![]() and
and ![]() . The frequency is 45.0 Hz.
. The frequency is 45.0 Hz.
Let kxmax be the beginning wavenumber for the evanescent energy.
We assign a weight of 1 to the wavenumbers smaller than kxmax
and a weight of 0.001 to the wavenumbers bigger than kxmax.
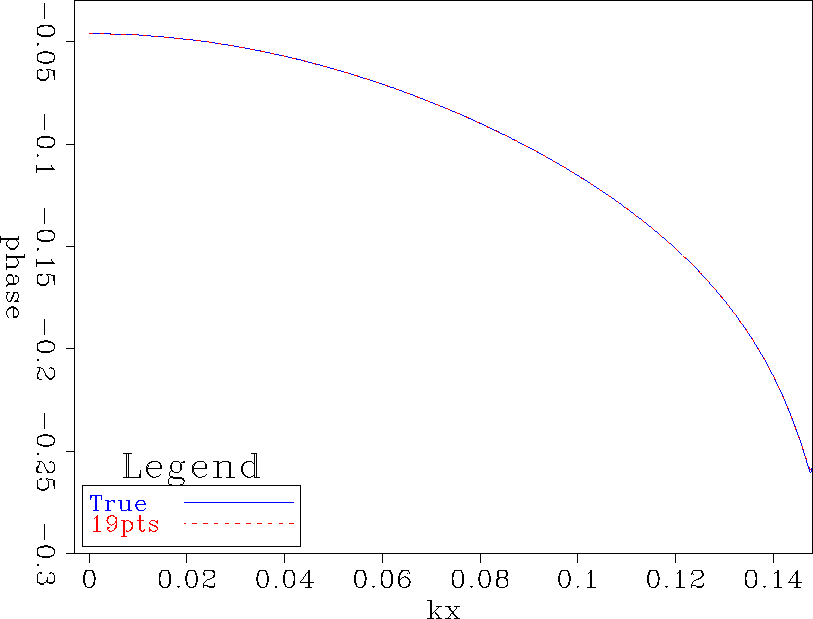
In Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the phase for the even part of the 19-point filter example is very close to the true operator.
In this model, the beginning wavenumber for the evanescent energy kxmax is 0.15.
In Figure
, the phase for the even part of the 19-point filter example is very close to the true operator.
In this model, the beginning wavenumber for the evanescent energy kxmax is 0.15.
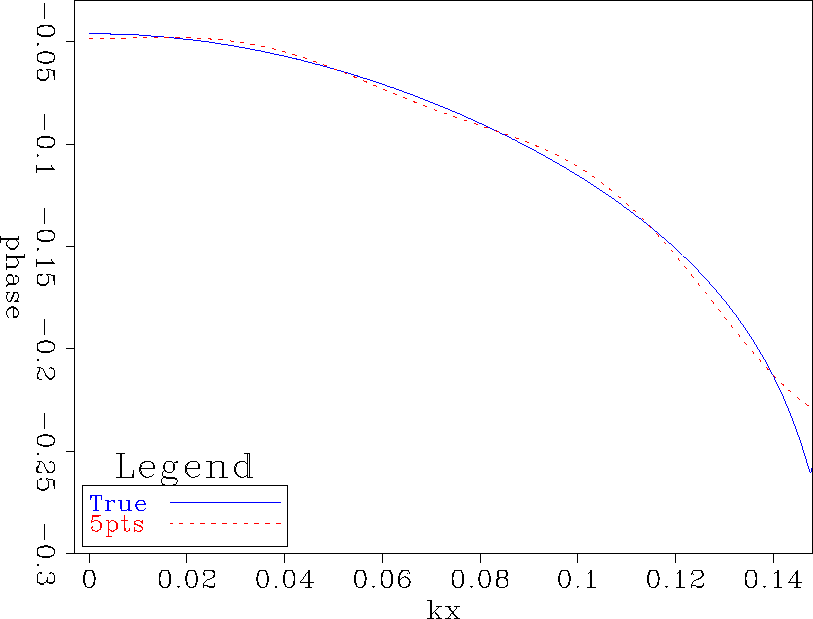
In Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the phase curve for the even part of the 5-point filter oscillates around the true operator.
The 5-point filter is not accurate even for the low wavenumber energy.
If our aim is to guarantee the accuracy
of the low-angle (low-wavenumber) energy, we can assign big weights to the low-angle energy
but small weights to the high-angle energy.
We can also smooth the amplitude and phase of the high angle-energy.
Now we assign a weight of 1 to the wavenumbers smaller than
, the phase curve for the even part of the 5-point filter oscillates around the true operator.
The 5-point filter is not accurate even for the low wavenumber energy.
If our aim is to guarantee the accuracy
of the low-angle (low-wavenumber) energy, we can assign big weights to the low-angle energy
but small weights to the high-angle energy.
We can also smooth the amplitude and phase of the high angle-energy.
Now we assign a weight of 1 to the wavenumbers smaller than
![]() and a weight of 0.001 to the wavenumbers bigger than
and a weight of 0.001 to the wavenumbers bigger than ![]() .In this model,
.In this model, ![]() is 0.125.
Figure
is 0.125.
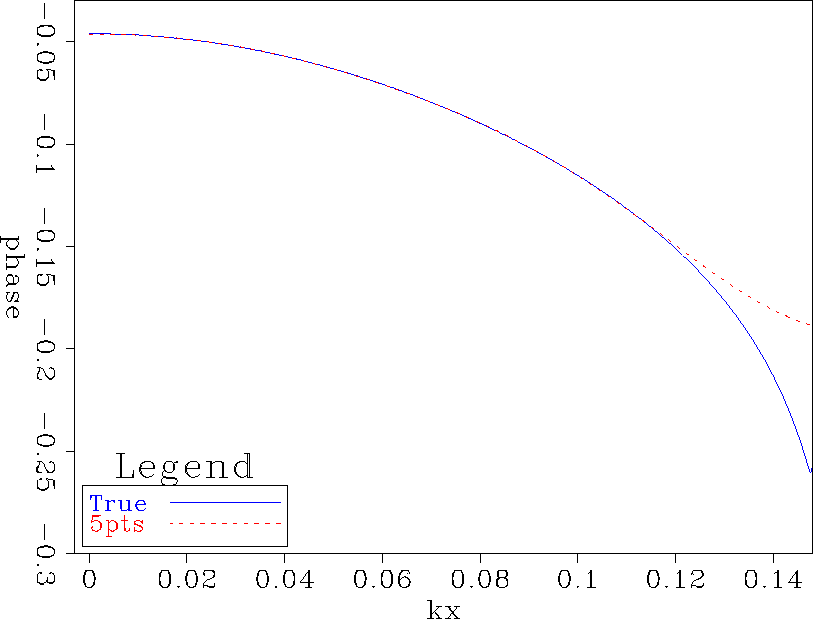
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the phase curve of the 5-point filter after we change the weighting policy.
The new 5-point filter is very close
to the true operator at the low wavenumbers (smaller than 0.12) but has a big error at the high wavenumbers.
shows the phase curve of the 5-point filter after we change the weighting policy.
The new 5-point filter is very close
to the true operator at the low wavenumbers (smaller than 0.12) but has a big error at the high wavenumbers.
 |
 |
 |
Though we lose the accuracy of high-angle energy when shorten the filter when we shorten the filter,
we greatly improve the efficiency of our algorithm.
If we use the 5-point filter in both inline and crossline directions in 3D wavefield extrapolation,
the correction operator is a ![]() 2D filter, while
it is a
2D filter, while
it is a ![]() 2D filter if we use the 19-point filter. Therefore using the 5-pointer filter,
computation cost for the convolution in 3D wavefield extrapolation is about
2D filter if we use the 19-point filter. Therefore using the 5-pointer filter,
computation cost for the convolution in 3D wavefield extrapolation is about ![]() the cost
using the 19-pointer filter. Furthermore, when the media is not homogeneous,
searching for the coefficients of a filter in the coefficient table plays an important role in 3D.
The total size of the coefficient table of the 5-point filter is about
the cost
using the 19-pointer filter. Furthermore, when the media is not homogeneous,
searching for the coefficients of a filter in the coefficient table plays an important role in 3D.
The total size of the coefficient table of the 5-point filter is about ![]() the size of
the 19-point filter in 3D. If we build the table with
100 discrete
the size of
the 19-point filter in 3D. If we build the table with
100 discrete ![]() s, 10 discrete
s, 10 discrete ![]() s and 10 discrete
s and 10 discrete ![]() s, the size of
table is about 8 Megabyte for the 5-point filter and is about 128 Megabyte for the 19-point filter. The speed
of searching in a 8 Megabyte is much faster than that in a 128 Megabyte table.
By shortening the filter, we can greatly reduce the cost for the explicit correction operator
in 3D wavefield extrapolation.
s, the size of
table is about 8 Megabyte for the 5-point filter and is about 128 Megabyte for the 19-point filter. The speed
of searching in a 8 Megabyte is much faster than that in a 128 Megabyte table.
By shortening the filter, we can greatly reduce the cost for the explicit correction operator
in 3D wavefield extrapolation.
We lose the accuracy of high-angle energy when we shorten the length of the filter. But we can apply plane-wave decomposition and tilted coordinates Shan and Biondi (2004a) to make the wavefield-extrapolation direction close to the direction of wave propagation. By doing this, we can get good accuracy for the high-angle energy even with a less accurate operator.