Computation of the vertical wavenumber

Equation (5) contains all the velocity information in the data and can be precomputed, at least in part. Notice that, although we described the algorithm for $n_v=n\mathbf{x}$, that is not necessary because the range of velocities is limited and independent of the spatial dimensions of the data (although the velocities themselves vary spatially).

Start by binning the velocities in small bins, for example at 10 m/s (which would imply a maximum velocity error of 5 m/s, well below the likely error in the estimation of the velocities themselves) such that the vertical wavenumber k_zl (that is, the dispersion relation), needs to be computed only a few hundred times and can thus be stored as a function of the horizontal wavenumber and the velocity. From the standpoint of the theoretical algorithm, all that changes is the selection process to choose the trace from the extrapolated wavefield that corresponds to the binned velocity at each spatial location. That is, instead of the selection being simply a multiplication by a Kronecker delta to choose l=j as it was before, it is now a multiplication with a Kronecker delta, to select l=p(j), that is, the wavefield that was migrated with the binned velocity corresponding to the bin of V(j). Equation (2) can then be rewritten as:

$$\mathbf{w}^{N+1}=\sum_{l=1}^{n_v}\mathbf{w}_l^{N+1}\sum_p\delta_{pl}.$$

The equation for the wavefield extrapolation then becomes:  

$$\mathbf{W}^{N+1}(j)=\sum_{m=1}^{n_x}\mathbf{W}^N(m)\sum_{l=1... ...k_{z_l}(m)\Delta z}\sum_pe^{-ik_x(\tilde{m}_j)\Delta x_p}\big).$$ (6)

Notice that summation over l involves summing over all the binned velocities whereas summation over p involves selecting the different wavefield components that correspond to a given velocity. That is, p ranges over the spatial locations whose binned velocity is V_l for each l. Figure  shows the velocity selection. This time, since we don't have a wavefield migrated with each velocity, at each spatial location, it is likely that several locations correspond to the same wavefield, since they correspond to the same velocity bin. There is, obviously, just one possible velocity at each spatial location, but many spatial locations may share the same velocity. Also, it is possible for a particular velocity not to be required at a specific depth step.

 

bin_vels2 Figure 2 Diagram illustrating velocity selection when there are fewer velocities than spatial locations.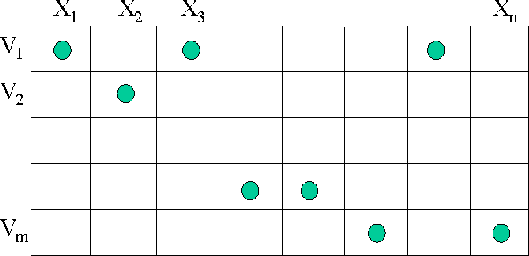