Next: Conclusions
Up: Rosales and Biondi: PS-COMAZ
Previous: Converted-wave common-azimuth migration
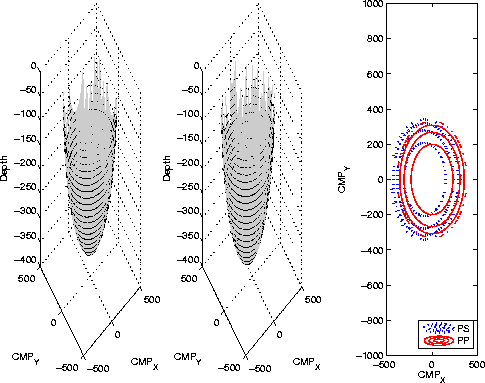
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents the summation surfaces
[equation (1)]
for an impulse response at a depth of 500 m, a P-velocity of 3000 m/s, an
S-velocity of 1500 m/s, and an in-line offset of 3000 m. The left panel
shows the single-mode PP summation surface, and the right panel shows the
converted-mode PS summation surface. Similarly, Figure
presents the summation surfaces
[equation (1)]
for an impulse response at a depth of 500 m, a P-velocity of 3000 m/s, an
S-velocity of 1500 m/s, and an in-line offset of 3000 m. The left panel
shows the single-mode PP summation surface, and the right panel shows the
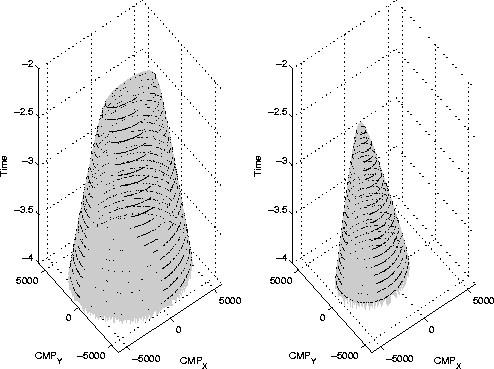
converted-mode PS summation surface. Similarly, Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the spreading surfaces; that is, the theoretical solution for depth
of equation (1), Appendix A shows the calculations.
The left panel presents the single-mode PP spreading surface, the center
panel shows the converted-mode PS spreading surface, and the right panel
compares the contour lines for both spreading surfaces.
shows the spreading surfaces; that is, the theoretical solution for depth
of equation (1), Appendix A shows the calculations.
The left panel presents the single-mode PP spreading surface, the center
panel shows the converted-mode PS spreading surface, and the right panel
compares the contour lines for both spreading surfaces.
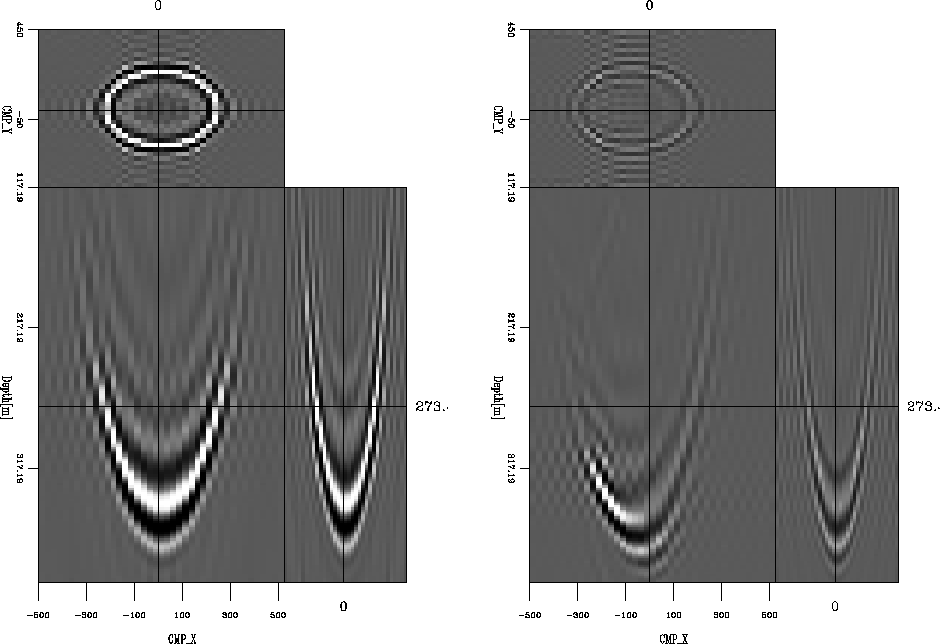
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the common-azimuth impulse response for a
constant P-velocity of 2500 m/s, and a constant
S-velocity of 1250 m/s, and an in-line offset of 200 m.
The left panel exhibits the response
for the single-mode PP common-azimuth migration operator, and the right
panel exhibits the response for the converted-mode PS
migration operator.
shows the common-azimuth impulse response for a
constant P-velocity of 2500 m/s, and a constant
S-velocity of 1250 m/s, and an in-line offset of 200 m.
The left panel exhibits the response
for the single-mode PP common-azimuth migration operator, and the right
panel exhibits the response for the converted-mode PS
migration operator.
impcheops
Figure 1
Summation surfaces for a constant medium with a of P-velocity of 3000 m/s, an
S velocity of 1500 m/s, and an offset of 2 km. Left: PP summation surface.
Right: PS summation surface.
|
|  |




 imptheory
imptheory
Figure 2
Spreading surfaces for an impulse at 0.320 s PP traveltime and 0.480 s PS traveltime,
an offset of 200 m, and assuming constant P-velocity of 2500 m and
S-velocity of 1250 m. Left: PP spreading surface. Center: PS spreading surface.
Right: contour lines comparison from both spreading
surfaces.





imp.resp
Figure 3
Impulse response for a point diffractor at 0.320 s PP traveltime and 0.480 s PS traveltime,
and in a constant-velocity medium with a P-velocity of 2500 m/s and S-velocity
of 1250 m/s. Left: presents the single-mode PP. Right: panel presents the
converted-mode PS.
|
|  |










Next: Conclusions
Up: Rosales and Biondi: PS-COMAZ
Previous: Converted-wave common-azimuth migration
Stanford Exploration Project
5/3/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the common-azimuth impulse response for a
constant P-velocity of 2500 m/s, and a constant
S-velocity of 1250 m/s, and an in-line offset of 200 m.
The left panel exhibits the response
for the single-mode PP common-azimuth migration operator, and the right
panel exhibits the response for the converted-mode PS
migration operator.
shows the common-azimuth impulse response for a
constant P-velocity of 2500 m/s, and a constant
S-velocity of 1250 m/s, and an in-line offset of 200 m.
The left panel exhibits the response
for the single-mode PP common-azimuth migration operator, and the right
panel exhibits the response for the converted-mode PS
migration operator.