Synthetic examples

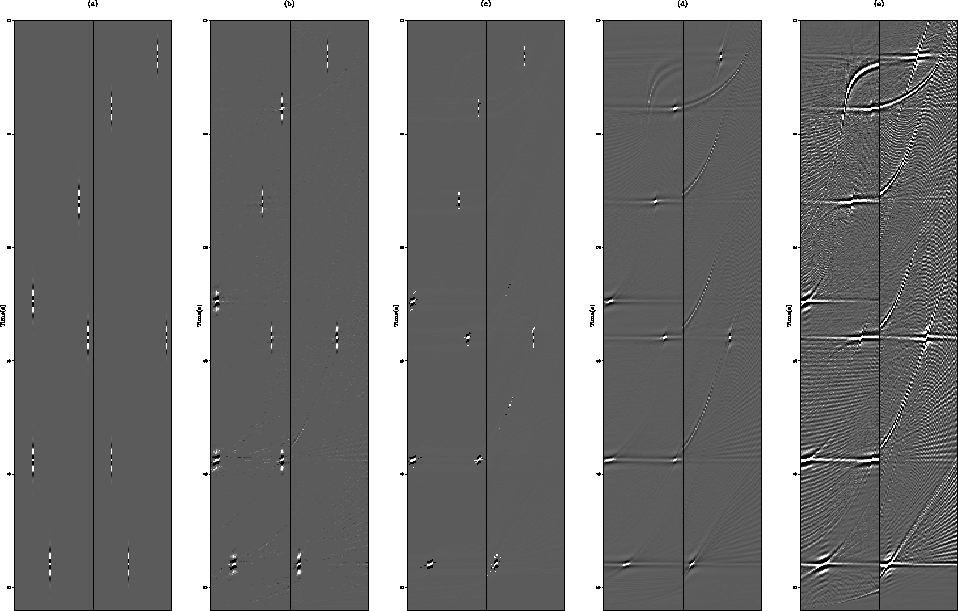
The first concern when solving inversion problems with over-complete dictionaries is the potential for introduction of cross-talk Claerbout (1992) into the model-space. A synthetic data set was created to test the method to assure that this technique does not allow this to happen. Figure shows the inverted models produced with the various methods compared to the least-squares solution. The first panel is a bandlimited model from which data were forward modeled, and the last four panels show the models produced by the various inversion procedures.

While the first two inversion schemes produce very sparse model-spaces with no cross-talk, the l₁ and l₂ products contain the familiar parabolas in the LRT domain due to data-space hyperbolas and ellipses in the HRT domain from the linear events in the data.

 

syn1
Figure 1 Synthetic model-space examples. The model-space contains both radon domains. Thus, half way across the slowness axis the plot changes from representing energy in the hyperbolic radon domain to events in the linear radon domain. The origin and sampling interval for both domains are the same in this example. Panel (a) is the band-limited model. Panel (b) shows the BC inversion result. Panel (c) shows the Cauchy result. Panel (d) shows the l₁ result. Panel (d) shows the l₂ result.

The models produced by all the results are very good. The clip level is deliberately set very low to bring out artifacts. While the first two methods produce very sparse results, the l₁ and l₂ results contain sweeping artifacts and readily identifiable cross-talk between the two model domains.

Figure shows the forward modeled data from the models produced from the various inversion techniques. The first panel is the starting data. Once again, the clip level has been set quite low to bring out the artifacts of the latter inversion schemes. Amazingly, the two sparse inversion schemes, especially the Cauchy inversion in panel (c), were able to remove much of the 0.000001 variance noise added to the data. A small amount of corrilary chatter can be seen in the Cauchy, l₁, and l₂ data domains linear.

 

syn2
Figure 2 Forward modeled data from the inversion results presented in Figure . Panel (a) is the band-limited model. Panel (b) shows the BC inversion result. Panel (c) shows the Cauchy result. Panel (d) shows the l₁ result. Panel (d) shows the l₂ result.

The inversion schemes designed for sparse model domains have produced models with no cross-talk between the two operators. The l₁ and l₂ inversions have allowed the transmission of energy between the two domains. However, the forward modeled data from all the methods show more than adequate results with only minor noise introduced in the immediate vicinity of the various events. Importantly, even the very steeply dipping events are well modeled despite being severely aliased. It should be noted however, that the first two schemes will not produce satisfactory data-space results given realistic split-spread gathers. Their short-comings are from linear events that do not continue completely across the entire data domain. The sparse model domains do not have sufficient freedom to add fictitious model energy to cancel events that do not exactly eminate from the origin of the shot (ie. exit the gather at t=0, x=0). Throughout this effort, only off-end gathers will be used.