 |
Figure 1 The herringbone data, (a) original data, and (b) data with hole.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
As a starting point, the hole was interpolated using a stationary PEF that was
![]() coefficients, shown in Figure
coefficients, shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a. We can see
how well the PEF has characterized the data by convolving the PEF with either
the original data or the interpolated result. The result of convolving the PEF
with the interpolated result is shown in Figure
a. We can see
how well the PEF has characterized the data by convolving the PEF with either
the original data or the interpolated result. The result of convolving the PEF
with the interpolated result is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b. As has
been previously noted, the PEF appears to miss the spines of the herringbone
pattern, but gets the two slopes relatively well. When examining the
result of random noise divided by that same stationary PEF (shown in Figure
b. As has
been previously noted, the PEF appears to miss the spines of the herringbone
pattern, but gets the two slopes relatively well. When examining the
result of random noise divided by that same stationary PEF (shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c)
we can see the problem with the assumption of stationarity in that the two slopes
present in the herringbone pattern are co-located throughout the simulation.
c)
we can see the problem with the assumption of stationarity in that the two slopes
present in the herringbone pattern are co-located throughout the simulation.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
The problems with co-located dips due to the assumption of stationarity can be
avoided by using a non-stationary PEF. A ![]() non-stationary PEF (with
a total of about 16,000 filter coefficients) was estimated on the known data
and then used to interpolate the missing data. As we can see from Figure
non-stationary PEF (with
a total of about 16,000 filter coefficients) was estimated on the known data
and then used to interpolate the missing data. As we can see from Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a, the result is nearly
perfect, which shouldn't be surprising given that the non-stationary PEF was
estimated on the answer. Still, the restored version appears to have little of
the problems of the interpolation smoothly decaying to zeros that was present in
the stationary case. When convolving the PEF with the full dataset, we can
see from the relative strength of the edge effects (in Figure
a, the result is nearly
perfect, which shouldn't be surprising given that the non-stationary PEF was
estimated on the answer. Still, the restored version appears to have little of
the problems of the interpolation smoothly decaying to zeros that was present in
the stationary case. When convolving the PEF with the full dataset, we can
see from the relative strength of the edge effects (in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b) that the filter perfectly
captured the data. When we remove the edge effects, we see no trace of the spine
of the herringbone, and the result looks very random as seen in Figure
b) that the filter perfectly
captured the data. When we remove the edge effects, we see no trace of the spine
of the herringbone, and the result looks very random as seen in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c.
c.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
The previous test was a demonstration of the effectiveness of a non-stationary PEF as a container for information, but we had the answer before attempting to solve the problem. Next, we must resolve the issue of non-stationary PEFs with holes in them, which happens when we do not have the answer.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
A more realistic starting point would be to estimate a PEF on the data with the
hole and hope that the regularization term in fitting goal (5)
would act as a method of interpolating the PEF in areas with missing data. As
we can see from the results in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , this is clearly
not the case. The restored data using a stationary PEF extends much further into
the gap than the non-stationary PEF does. If we look at the model residual from fitting
goal (5) shown in Figures
, this is clearly
not the case. The restored data using a stationary PEF extends much further into
the gap than the non-stationary PEF does. If we look at the model residual from fitting
goal (5) shown in Figures
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) e and f, we
can start to see why. This is a portion of the model residual for two
non-stationary filter coefficients over
the entire space of the non-stationary PEF. We can see that as we move within the
gap that the residual drops to zero, as the filter coefficients are also zero
within this area. Relying upon the filter regularization to fill in
gaps in the non-stationary filter does not put filters in holes.
e and f, we
can start to see why. This is a portion of the model residual for two
non-stationary filter coefficients over
the entire space of the non-stationary PEF. We can see that as we move within the
gap that the residual drops to zero, as the filter coefficients are also zero
within this area. Relying upon the filter regularization to fill in
gaps in the non-stationary filter does not put filters in holes.
We can also look at the performance of the PEFs by looking at the random
realizations as well as random noise divided by the non-stationary PEF, both shown in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . These results mostly confirm what we already know from
Figure
. These results mostly confirm what we already know from
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , however it is surprising to see that
Figures
, however it is surprising to see that
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b and c, which use the full data, are not as consistent as expected.
The areas which contain the herringbone pattern are non consistent from simulation
to simulation. This is not the case with the stationary PEF result of
Figure
b and c, which use the full data, are not as consistent as expected.
The areas which contain the herringbone pattern are non consistent from simulation
to simulation. This is not the case with the stationary PEF result of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c.
c.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
Instead of interpolating filter coefficients by relying on an isotropic
roughener for regularization, a much simpler approach is taken. After the
non-stationary PEF is estimated, the filter coefficients in areas with
missing data are simply interpolated in a nearest-neighbor fashion
with the nearest filter coefficients that are constrained by data.
The results of using this method are shown in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . On the first panel (a), we can see that the signal
that we want to destroy with our filter is partially gone, and the
output looks much more random than before. On the second panel (b), we see that the
interpolated result is better than any of the previous attempts.
While there is only a single dip in any location, these dips are not
in the correct locations as they do not follow the vertical spine of
the herringbone. On the third panel (c), a single filter lag plotted
with respect to space, we can clearly see the
difference between filter coefficients that have been estimated on
data, and those that have been interpolated from neighboring area with data.
. On the first panel (a), we can see that the signal
that we want to destroy with our filter is partially gone, and the
output looks much more random than before. On the second panel (b), we see that the
interpolated result is better than any of the previous attempts.
While there is only a single dip in any location, these dips are not
in the correct locations as they do not follow the vertical spine of
the herringbone. On the third panel (c), a single filter lag plotted
with respect to space, we can clearly see the
difference between filter coefficients that have been estimated on
data, and those that have been interpolated from neighboring area with data.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
If we examine the mappings between the areas with no data and their
nearest neighbors as shown in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a and b, we
can see that the mappings do not correspond to the vertical trend
present in the herringbone data. If we alter the nearest-neighbor
interpolation so that no points outside of the vertical direction are
considered, with the result shown in Figures
a and b, we
can see that the mappings do not correspond to the vertical trend
present in the herringbone data. If we alter the nearest-neighbor
interpolation so that no points outside of the vertical direction are
considered, with the result shown in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c and d.
c and d.
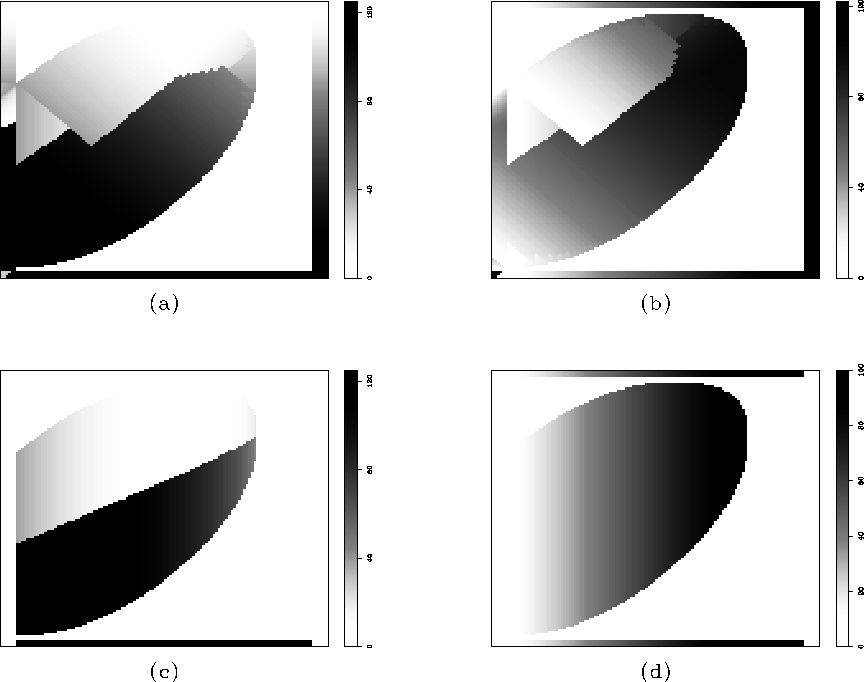 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
In addition to changing the filter interpolation so that it acts in a
preferential direction, the regularization of the filter has been
changed from an isotropic Laplacian to a derivative in the vertical
direction. The results of using both of these new methods is shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The first panel (a) shows how the missing
signal is better attenuated with this method. The second panel (b) is
the interpolation result, which is far superior to any other method
shown in this paper. The correct dips are present in the correct
locations. The amplitude of the interpolated result is not as uniform
as would be desired, however. Finally, in the third panel (c), we can
see that the interpolated filter coefficients are much more difficult
to identify than with the previous method. The only obvious
artifact is the seam caused by the nearest-neighbor interpolation
when the interpolated data switched from one side of the gap to the other.
. The first panel (a) shows how the missing
signal is better attenuated with this method. The second panel (b) is
the interpolation result, which is far superior to any other method
shown in this paper. The correct dips are present in the correct
locations. The amplitude of the interpolated result is not as uniform
as would be desired, however. Finally, in the third panel (c), we can
see that the interpolated filter coefficients are much more difficult
to identify than with the previous method. The only obvious
artifact is the seam caused by the nearest-neighbor interpolation
when the interpolated data switched from one side of the gap to the other.
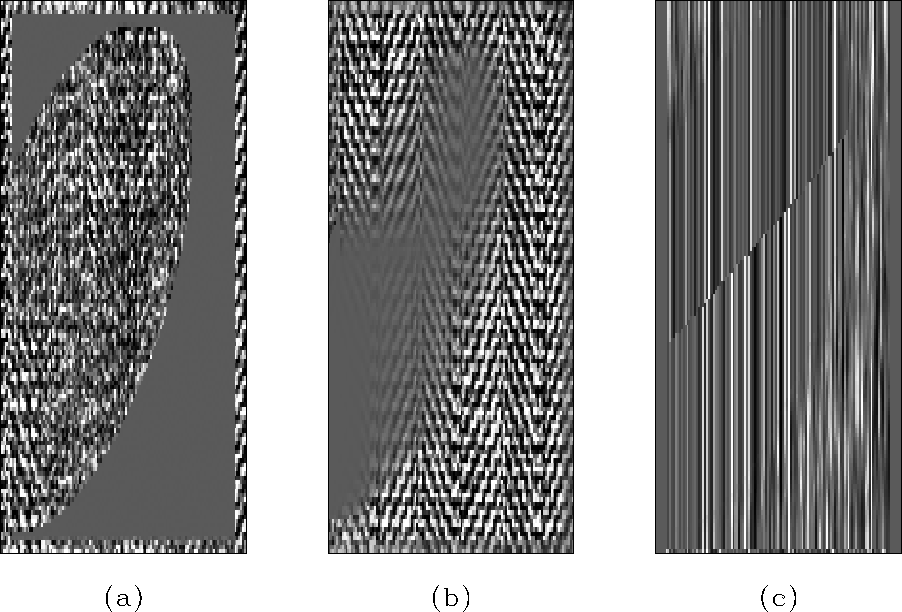 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . (b) Interpolation
with the PEF. Again, the result is better than in Figure
. (b) Interpolation
with the PEF. Again, the result is better than in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The dips are all in the correct locations,
but the amplitude is not as high as it should be. (c) Filter
coefficients from a single filter lag. The nearest-neighbor
interpolated filter coefficients are now much harder to distinguish
from the area where the PEF is estimated from local data.
. The dips are all in the correct locations,
but the amplitude is not as high as it should be. (c) Filter
coefficients from a single filter lag. The nearest-neighbor
interpolated filter coefficients are now much harder to distinguish
from the area where the PEF is estimated from local data.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)