




Next: Examples
Up: Guitton: High resolution Radon
Previous: The L-BFGS-B algorithm
Given a CMP gather 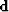 and a radon transform operator
and a radon transform operator 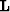 , we want to minimize the least-squares objective function
, we want to minimize the least-squares objective function
| 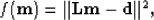 |
(3) |
where 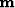 is the unknown radon domain. The main idea of this
paper is to decompose
is the unknown radon domain. The main idea of this
paper is to decompose 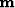 into its positive and negative parts
by imposing simple bounds on
into its positive and negative parts
by imposing simple bounds on 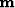 with the L-BFGS-B
algorithm. Therefore, the two problems
with the L-BFGS-B
algorithm. Therefore, the two problems
| ![\begin{displaymath}
\mbox{ min } f({\bf m_{(-)}})\mbox{ subject to }{\bf m_{(-)}}\in\;\;]-\infty,0[ \;\;,\end{displaymath}](img10.gif) |
(4) |
and
| 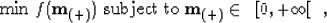 |
(5) |
need to be solved. Note that we could decompose 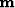 into more
subdomains as well. It is important to solve both problems of finding
into more
subdomains as well. It is important to solve both problems of finding
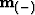 and
and 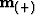 independently, and not
simultaneously as it can be done with linear programming techniques
Claerbout and Muir (1973).
Here, the main idea is to decrease the null space
and its effects by constraining the model, similar to what is
accomplished with the Cauchy regularization. Once the two models
independently, and not
simultaneously as it can be done with linear programming techniques
Claerbout and Muir (1973).
Here, the main idea is to decrease the null space
and its effects by constraining the model, similar to what is
accomplished with the Cauchy regularization. Once the two models 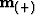 and
and 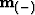 are estimated with the L-BFGS-B algorithm,
the sparse model is obtained by computing
are estimated with the L-BFGS-B algorithm,
the sparse model is obtained by computing 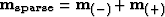 .
In the following section, I illustrate this technique with a synthetic
and real data example using the hyperbolic radon transform.
.
In the following section, I illustrate this technique with a synthetic
and real data example using the hyperbolic radon transform.





Next: Examples
Up: Guitton: High resolution Radon
Previous: The L-BFGS-B algorithm
Stanford Exploration Project
5/3/2005