Linear least-squares inversion

Tarantola (1987) formalizes the geophysical inverse problem by giving a theoretical approach to compensate for the experiment's deficiencies (e.g., acquisition geometry, obstacles), while being consistent with the acquired data. His approach can be summarized as follows: given a linear modeling operator 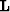${\bf L}$ to compute synthetic data d,

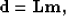$${\bf d}={\bf L}{\bf m},$$ (1)

where m is a reflectivity model, and given the recorded data 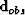${\bf d}_{obs}$, a quadratic cost function,

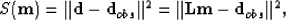$$S({\bf m})=\Vert {\bf d} - {\bf d}_{obs} \Vert^2 =\Vert {\bf L}{\bf m} - {\bf d}_{obs} \Vert^2,$$ (2)

is formed. The model of the earth 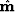$\hat {\bf m}$ that minimize $S({\bf m})$ is given by

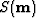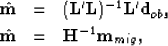$$\begin{eqnarray} \hat{{\bf m}}&=&({\bf L}'{\bf L})^{-1}{\bf L}' {\bf d}_{obs} \\ \hat{{\bf m}}&=& {\bf H}^{-1} {\bf m}_{mig}, \end{eqnarray}$$ (3) (4)

where 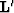${\bf L}'$ (migration operator) is the adjoint of the linear modeling operator 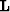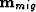${\bf L}$, ${\bf m}_{mig}$ is the migration image, and 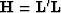${\bf H}={\bf L}'{\bf L}$ is the Hessian of $S({\bf m})$.

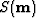The main difficulty with this approach is the explicit calculation of the Hessian inverse. In practice, it is more feasible to compute the least-squares inverse image as the solution of the linear system of equations  

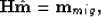$${\bf H} \hat{{\bf m}}={\bf m}_{mig},$$ (5)

by using an iterative conjugate gradient algorithm.

Another difficulty with this approach is that the explicit calculation of the Hessian for the entire model space is unfeasible in practice. In the next section we discuss a way to overcome this problem.