Examples

I illustrate the higher-order RWE extrapolators with impulse responses for two models with increasing levels of complexity.

The first example is based on a model with two smooth velocity anomalies that generate focusing and defocussing of the coordinate system, without triplication. I construct the coordinate system by ray tracing from an incident horizontal plane-wave at the surface. Figure   shows the velocity model with the coordinate system overlayed. Figure   shows the coordinate system coefficients defined in equation (9).

 

RWEimp0.cos Figure 1 Velocity map and Riemannian coordinate system.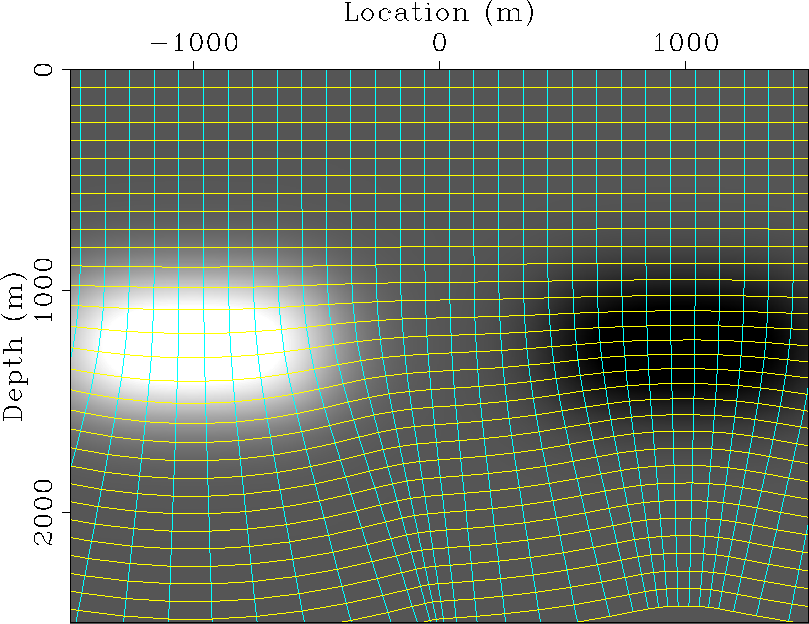

The goal of this test model is to illustrate the higher-order extrapolation kernels in a fairly simple coordinate system which is close to a Cartesian basis. The coordinate system is constructed from an incident plane wave, while the data comes from a point source. This setting is almost identical to the case of extrapolation from a point source in Cartesian coordinates, where high-angle propagation requires high-order kernels. In this case, the Riemannian coordinate system does not match closely the general direction of wave propagation, so higher order kernels are needed. In practice, this situation can be addressed better with synthesized plane-wave data extrapolated in a coordinate system ray traced from an incident plane, and with point source data extrapolated in a coordinate system ray traced from a point source.

 

RWEimp0.ab
Figure 2 (a) Parameter $a=s \aa$ in ray coordinates. (b) Parameter $b=\aa/J$ in ray coordinates.

Figure   shows the velocity model and impulse responses for a point source computed with various extrapolators in ray coordinates ($\tau$ and $\gamma$). Panel (a) shows the slowness model, panel (b) shows extrapolation with the $15^\circ$ finite-differences equation, panel (c) shows extrapolation with the $45^\circ$ finite-differences equation, panel (d) shows extrapolation with the split-step Fourier (SSF) equation, panel (e) shows extrapolation with the pseudo-screen (PSC) equation, and panel (f) shows extrapolation with the Fourier finite-differences (FFD) equation. All plots are displayed in ray coordinates. We can observe that the angular accuracy of the extrapolator improves for the more accurate extrapolators. The finite-differences solutions (panels b and c) show the typical behavior of such solutions for the $15^\circ$ and $45^\circ$ equations (e.g. the cardioid for $45^\circ$), but in the more general setting of Riemannian extrapolation. The mixed-domain extrapolators (panels d, e, and f) show increased accuracy. The main differences occur at the highest propagation angles, and the most accurate extrapolators of those compared is the equivalent of Fourier finite-differences (panel f).

Figure   shows the corresponding plots in Figure   mapped in the physical coordinates, except for panel (a) which in this case shows the impulse response for extrapolation in Cartesian coordinates using a Fourier finite-differences extrapolator with a $15^\circ$ finite-differences term. The overlay is an outline of the extrapolation coordinate system. After re-mapping to the physical space, the comparison of high-angle accuracy for the various extrapolators is more obvious, since it now has the proper physical meaning.

 

RWEimp0.rweimg
Figure 3 (a) Slowness. (b) Extrapolation with the $15^\circ$ finite-differences equation. (c) Extrapolation with the $45^\circ$ finite-differences equation. (d) Extrapolation with the split-step Fourier (SSF) equation. (e) Extrapolation with the pseudo-screen (PSC) equation. (f) Extrapolation with the Fourier finite-differences (FFD) equation.

 

RWEimp0.carimg
Figure 4 (a) Extrapolation with the Fourier finite-differences (FFD) equation in Cartesian coordinates. (b) Extrapolation with the $15^\circ$ finite-differences equation. (c) Extrapolation with the $45^\circ$ finite-differences equation. (d) Extrapolation with the split-step Fourier (SSF) equation. (e) Extrapolation with the pseudo-screen (PSC) equation. (f) Extrapolation with the Fourier finite-differences (FFD) equation.

The second example is based on a model with a large lateral gradient which makes an incident plane wave overturn. A small Gaussian anomaly forces the coordinate system to focus slightly, and another large Gaussian anomaly, not used for the coordinate system, forces the propagating wave to triplicate and move at high angles relative to the extrapolation direction. Figure   shows the velocity model with the coordinate system overlayed. Figure   shows the coordinate system coefficients defined in equation (9).

 

RWEimp1.cos Figure 5 Velocity map and Riemannian coordinate system.

The goal of this model is to illustrate Riemannian wavefield extrapolation in a situation which cannot be handled correctly by Cartesian extrapolation, no matter how accurate. In this example, an incident plane wave is overturning, thus becoming evanescent for the solution in Cartesian coordinates. Furthermore, the large Gaussian anomaly, Figure  (a), causes serious wavefield triplication, thus requiring high-order kernels in the Riemannian extrapolator.

Figure   shows the velocity model and impulse responses for an incident plane wave computed with various extrapolators in ray coordinates ($\tau$ and $\gamma$). Panel (a) shows the slowness model, panel (b) shows extrapolation with the $15^\circ$ finite-differences equation, panel (c) shows extrapolation with the $45^\circ$ finite-differences equation, panel (d) shows extrapolation with the split-step Fourier (SSF) equation, panel (e) shows extrapolation with the pseudo-screen (PSC) equation, and panel (f) shows extrapolation with the Fourier finite-differences (FFD) equation. All plots are displayed in ray coordinates. As with the preceding example, we can observe increased angular accuracy as we increase the order of the extrapolator. The equivalent FFD is the most accurate.

As in the preceding example, Figure   shows the corresponding plots in Figure   mapped in the physical coordinates, except for panel (a) which in this case shows the impulse response for extrapolation in Cartesian coordinates using a Fourier finite-differences extrapolator with a $15^\circ$ finite-differences term. The overlay is an outline of the extrapolation coordinate system.

 

RWEimp1.ab
Figure 6 (a) Parameter $a=s \aa$ in ray coordinates. (b) Parameter $b=\aa/J$ in ray coordinates.

Panel (a) in Figure   clearly shows the failure of the Cartesian extrapolator in propagating waves correctly even up to $90^\circ$. All Riemannian extrapolators handle better the overturning waves, including energy that is propagating upward relative to the physical coordinates. As expected, the higher order kernels are more accurate in describing the triplicating wavefields.

 

RWEimp1.rweimg
Figure 7 (a) Slowness. (b) Extrapolation with the $15^\circ$ finite-differences equation. (c) Extrapolation with the $45^\circ$ finite-differences equation. (d) Extrapolation with the split-step Fourier (SSF) equation. (e) Extrapolation with the pseudo-screen (PSC) equation. (f) Extrapolation with the Fourier finite-differences (FFD) equation.

 

RWEimp1.carimg
Figure 8 (a) Extrapolation with the Fourier finite-differences (FFD) equation in Cartesian coordinates. (b) Extrapolation with the $15^\circ$ finite-differences equation. (c) Extrapolation with the $45^\circ$ finite-differences equation. (d) Extrapolation with the split-step Fourier (SSF) equation. (e) Extrapolation with the pseudo-screen (PSC) equation. (f) Extrapolation with the Fourier finite-differences (FFD) equation.