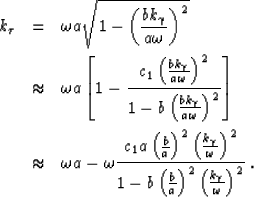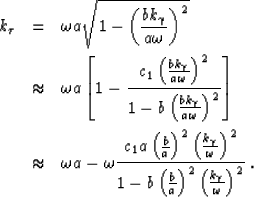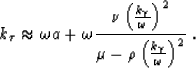Space-domain finite-differences

Starting from equation (9), based on the Muir expansion for the square-root Claerbout (1985), we can write successively:

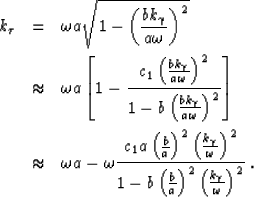$$\begin{eqnarray} k_\tau&=& \omega a \sqrt{1- \left (\frac{b k_\gamma}{a \omega}\... ...c{b }{a }\right )^2\left (\frac{ k_\gamma}{ \omega}\right )^2} \;.\end{eqnarray}$$ (19) (20) (21)

If we make the notations

$$\left\{ \begin{array} {l} \nu = - c_1a \left (\frac{b }{a }\... ...\\ \rho= b\left (\frac{b }{a }\right )^2\;. \end{array}\right.$$ (22)

we obtain the finite-differences solution to the one-way wave equation in Riemannian coordinates:

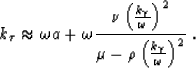$$k_\tau\approx \omega a + \omega\frac{ \nu \left (\frac{ k_\g... ... )^2} {\mu-\rho\left (\frac{ k_\gamma}{ \omega}\right )^2} \;.$$ (23)