Next: Conclusions and Future work
Up: Rosales and Sava: MAIS
Previous: Methodology
The Mahogany field, located in the Gulf of Mexico, is dominated by a salt body
structure. One of the data set acquired on this area consists on a 2-D Ocean Bottom Seismic (OBS)
multicomponent line. Rosales and Guitton (2004) present the steps involved in the
PZ summation that results in the P component section that is now under study.
The PZ summation was successful in eliminating the receiver ghost; however, other surface-related
multiples, like the source pegleg, are still present after the combination.
The remaining multiples are a problem when performing any migration-velocity-analysis
technique. Therefore, we apply the methodology discussed in the previous section to
eliminate the remaining multiples.
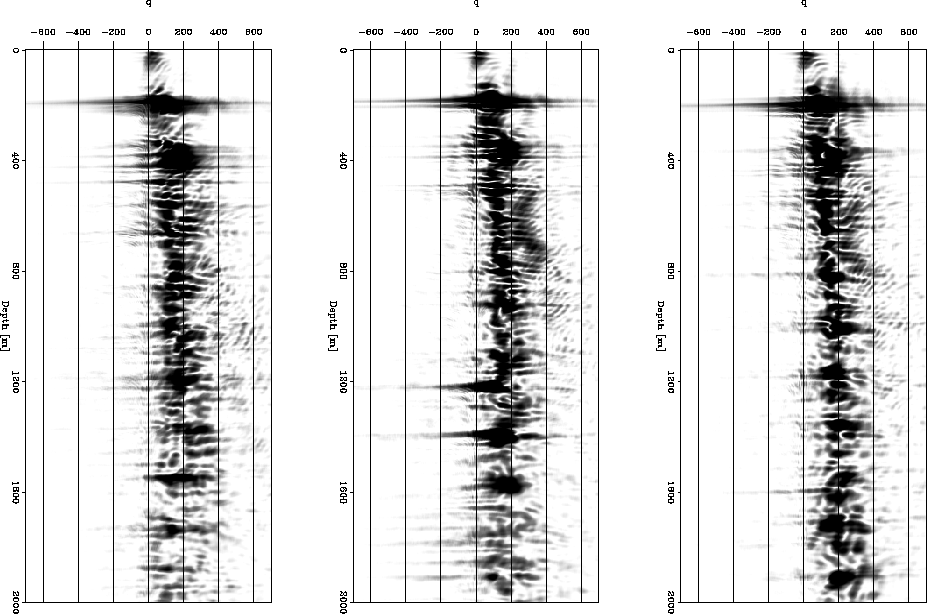
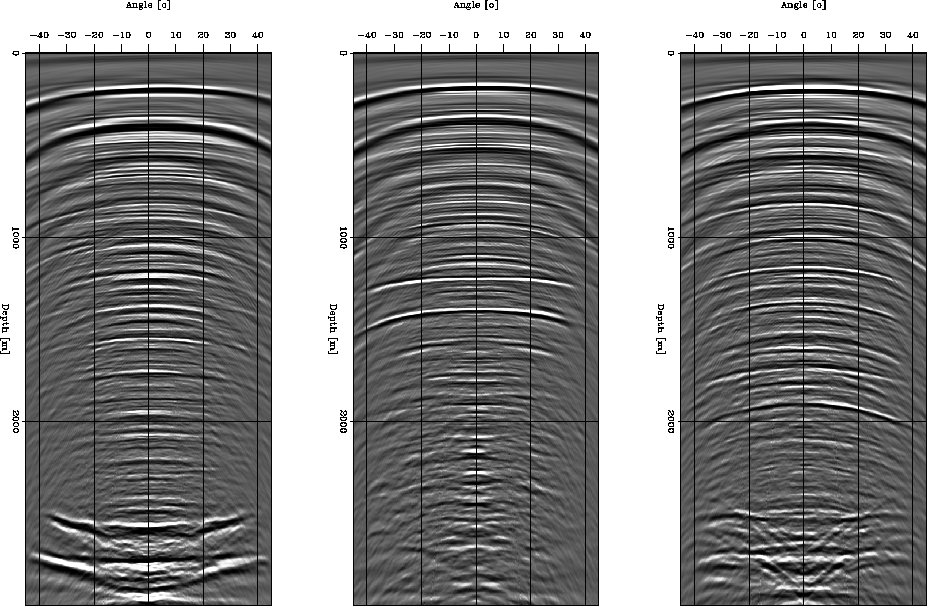
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows three characteristic angle-domain common-image gathers,
after three processes: the PZ summation described in Rosales and Guitton (2004), the downward continuation
of the sources to the receiver label, and the migration with the velocity model presented in
Rosales and Guitton (2004).
shows three characteristic angle-domain common-image gathers,
after three processes: the PZ summation described in Rosales and Guitton (2004), the downward continuation
of the sources to the receiver label, and the migration with the velocity model presented in
Rosales and Guitton (2004).
adcigs
Figure 2 ADCIGS after PZ summation at three different locations.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





It is possible to observe a similar residual curvature for both primaries and multiples. Additionally,
at this stage the primaries and multiples present
a very similar moveout, since the migration velocity is still not perfect. Any migration-velocity-analysis
technique done with this data will be biased with the multiple reflections still present.
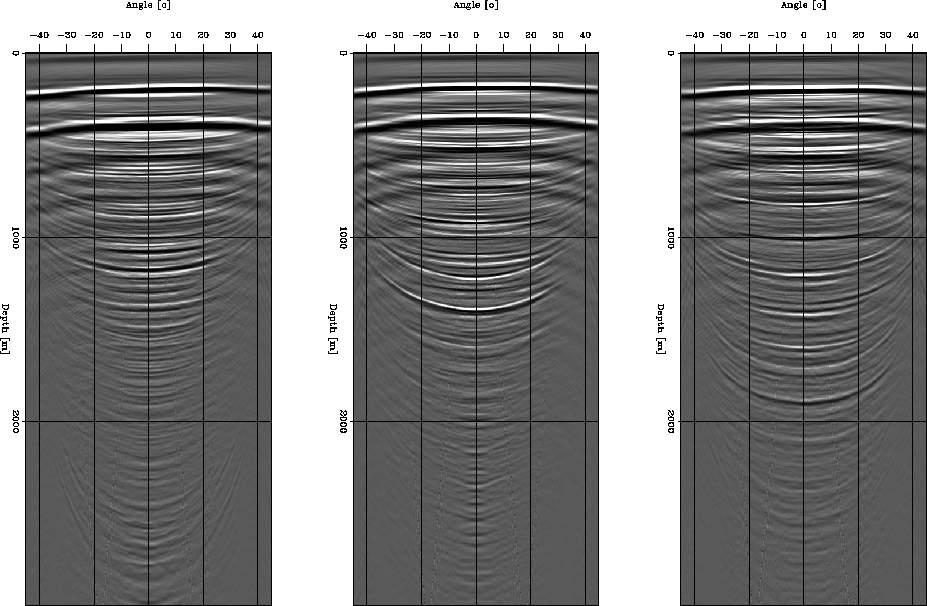
Additionally, Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents the same ADCIGs as in Figure
presents the same ADCIGs as in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) but after Radon transform in the angle domain is not easy to distinguish between primaries and multiples;
therefore, another process is required.
but after Radon transform in the angle domain is not easy to distinguish between primaries and multiples;
therefore, another process is required.
adcigs.art
Figure 3 ADCIGs in the Radon domain, before any residual curvature
process.





A residual curvature process will help to separate primaries and multiples in the Radon domain.
The advantage of using residual migration (as discussed on the methodology) over residual moveout
is that residual migration reduces the effects of image-point dispersal between events imaged at the
same physical location but with different aperture angle Biondi (2004).
Performing SRM with a value of 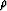 different than 1 (e.g.,
different than 1 (e.g., 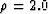 ) produces a distinct
difference between the residual moveouts of the
primaries and multiples. Figure
) produces a distinct
difference between the residual moveouts of the
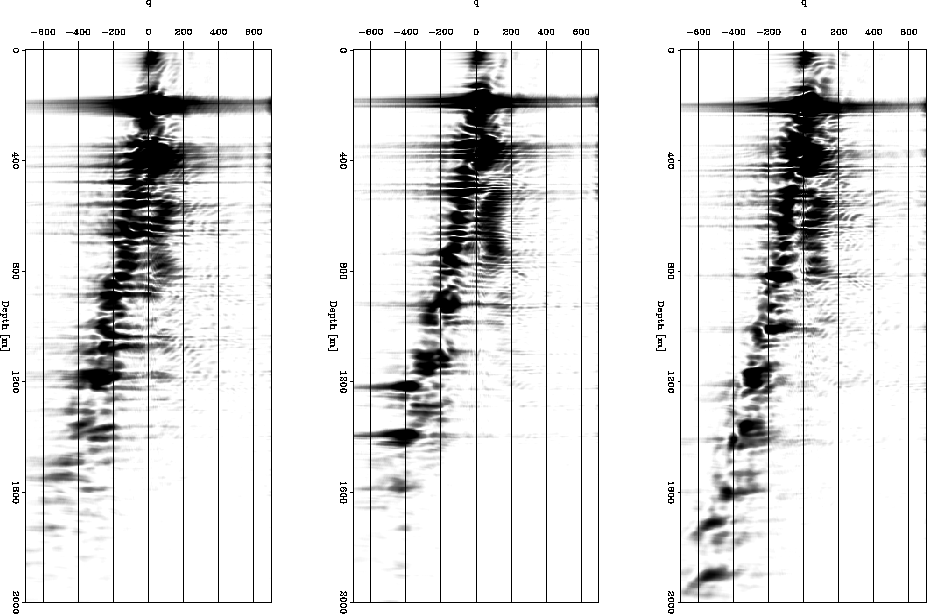
primaries and multiples. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the same ADCIGs as in Figure
shows the same ADCIGs as in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) after SRM with
after SRM with 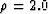 . It is now easy to distinguish between primaries and multiples through
their distinctive curvatures.
. It is now easy to distinguish between primaries and multiples through
their distinctive curvatures.
adcigs.srm
Figure 4 ADCIGs after SRM with 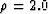 .
.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





Applying the Radon transform splits the image into two different curvatures;
therefore, it is possible to distinguish between
primaries (positive curvature) and multiples (negative curvature); additionally, it is possible to apply
principles and techniques similar to those discussed by Sava and Guitton (2003) or
Alvarez et al. (2004).
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ADCIGs in the Radon domain. After SRM is possible to
distinguish between primaries and multiples, compare the results on Figures
shows the ADCIGs in the Radon domain. After SRM is possible to
distinguish between primaries and multiples, compare the results on Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Figure
.
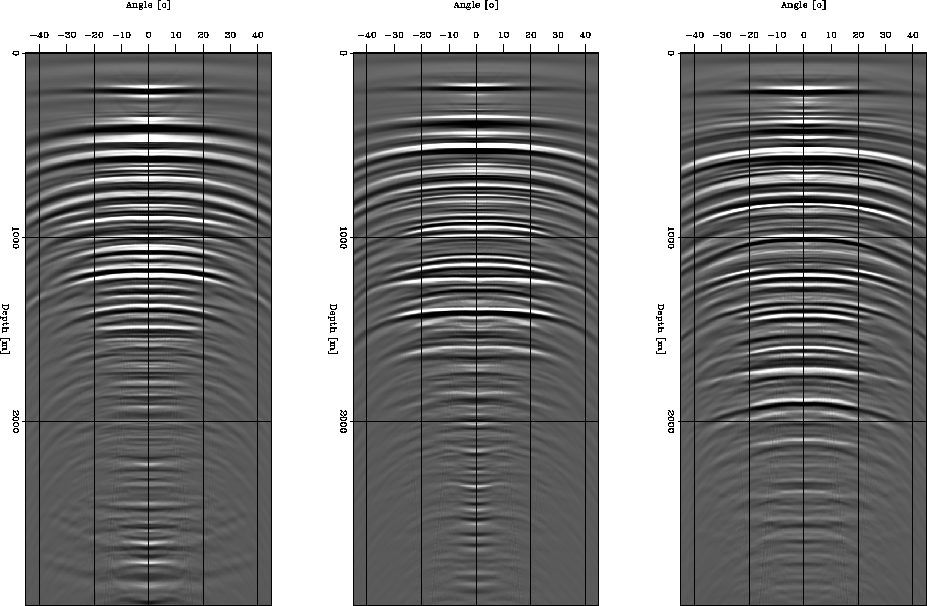
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents the result
after eliminating the multiples and applying SRM with a
presents the result
after eliminating the multiples and applying SRM with a 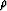 value of
value of 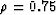 ;
this result shows a satisfactory elimination of multiples.
;
this result shows a satisfactory elimination of multiples.
adcigs.srm.art
Figure 5 ADCIGs after SRM in the Radon domain. Compare with
the ADCIGs in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and note how multiples and primaries are split into
two different trends.
and note how multiples and primaries are split into
two different trends.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





adcigs.srm.art.isrm
Figure 6 ADCIGS after multiple suppression.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: Conclusions and Future work
Up: Rosales and Sava: MAIS
Previous: Methodology
Stanford Exploration Project
10/23/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows three characteristic angle-domain common-image gathers,
after three processes: the PZ summation described in Rosales and Guitton (2004), the downward continuation
of the sources to the receiver label, and the migration with the velocity model presented in
Rosales and Guitton (2004).
shows three characteristic angle-domain common-image gathers,
after three processes: the PZ summation described in Rosales and Guitton (2004), the downward continuation
of the sources to the receiver label, and the migration with the velocity model presented in
Rosales and Guitton (2004).
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)