




Next: Multiple realization methodology
Up: Review
Previous: Review
In order to use this methodology
our tomography problem has to be set up in a similar
fashion to that of fitting goals (3).
This isn't necessarily straight forward.
Our first problem is that
tomography is a non-linear process.
The standard approach in ray-based tomography
is to linearize around an initial slowness
model 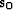 . Our linearized
tomography operator
. Our linearized
tomography operator 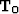 is formed by
rays traced through the background slowness.
We then write a linear relation between
the change in slowness
is formed by
rays traced through the background slowness.
We then write a linear relation between
the change in slowness 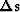 and the change
in travel-time
and the change
in travel-time 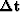 .
.
When doing migration velocity analysis
in the depth domain, we are not dealing
with travel-times but instead move-out
as a function of some parameter (offset
or azimuth) Stork (1992). Biondi and Symes (2003)
showed how for angle domain migration there
is a link between travel-time error dt,
local dip 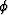 , the local slowness s
depth of the reflection z, the reflection angle
, the local slowness s
depth of the reflection z, the reflection angle 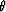 ,and scaling
,and scaling 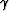 of the background slowness model.
This relation can be written in terms of an operator
of the background slowness model.
This relation can be written in terms of an operator 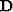 which maps from
which maps from 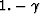 to
to 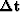 and whose elements are
and whose elements are
| 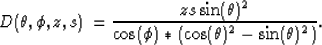 |
(4) |
For our regularization operator we can use a steering filter
Clapp et al. (1997); Clapp (2001a) oriented along reflector dips. Our
basic linearized fitting goals become
| 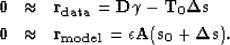 |
(5) |
| |
The added term in our regularization fitting goal 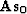 is due to the fact that we want to smooth slowness not change
in slowness. Clapp (2003a) and () showed
that adding noise to
is due to the fact that we want to smooth slowness not change
in slowness. Clapp (2003a) and () showed
that adding noise to 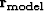 produced velocity models
with what looked like thin layers that had little effect on
image kinematics but noticeable effects on amplitudes.
produced velocity models
with what looked like thin layers that had little effect on
image kinematics but noticeable effects on amplitudes.
We run into problems when we want to explore
the effect of adding noise to 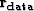 .Our
.Our 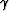 values, and therefore our data
fitting error exist in some irregular space (potentially
consistent angle sampling, but irregular
in space).
This makes making an effective noise covariance
operator difficult.
values, and therefore our data
fitting error exist in some irregular space (potentially
consistent angle sampling, but irregular
in space).
This makes making an effective noise covariance
operator difficult.





Next: Multiple realization methodology
Up: Review
Previous: Review
Stanford Exploration Project
10/23/2004
![]() , the local slowness s
depth of the reflection z, the reflection angle
, the local slowness s
depth of the reflection z, the reflection angle ![]() ,and scaling
,and scaling ![]() of the background slowness model.
This relation can be written in terms of an operator
of the background slowness model.
This relation can be written in terms of an operator ![]() which maps from
which maps from ![]() to
to ![]() and whose elements are
and whose elements are
![]() .Our
.Our ![]() values, and therefore our data
fitting error exist in some irregular space (potentially
consistent angle sampling, but irregular
in space).
This makes making an effective noise covariance
operator difficult.
values, and therefore our data
fitting error exist in some irregular space (potentially
consistent angle sampling, but irregular
in space).
This makes making an effective noise covariance
operator difficult.