




Next: Solver
Up: Abstract Classes
Previous: Vectors and super vectors
When it comes to writing an object oriented conjugate gradient
based inversion library there are two schools of thought.
One is a Bayesian approach that correlates vectors with their
decorrelators. In the Bayesian approach, Harlan (2004a,b)
being one example,
an inverse covariance function is associated with each vector. The
approach taken in this library,
and the approach taken by Gockenbach and Symes (1999) among others,
think more in terms of operators. Operators know
the space that their domain and range vectors reside in.
For this library I took the latter approach. My decision
was based more on code complexity issue more than anything else.
When building complex inversion operators, the programmer
has to be much more careful if the component operators
do not know the space of their domain and range vectors.
The abstract class SEP.operator.operator is
initialized with a string descriptor, domain vector, and a range vectors.
The space
these vectors exist in are stored in the operator.
The operator has several additional functions.
- init_op(restart)
- Initialize the operator.
- job_desc(iter)
- Return an ASCII string describing the operator given the current iteration. This will be used to keep track of the progress
of the inversion.
- forward_op(model,data,add,restart)
- Run the forward operation possibly by adding to the data, and with
the ability to signify a restart of the operation.
- adjoint_op(model,data,add,restart)
- Run the adjoint operation possibly by adding to the model, and with
the ability to signify a restart of the operation.
- check_operator(domain,range)
- A function to check to make sure
the domain and range vector conform to the domain and range vectors with which
the operator was initialized.
- forward(domain,range,status,iter,add,restart)
- A wrapper for running the forward operation. The additional
status and iter parameters are used to record the starting
and finished of forward operation to enable restarting.
- adjoint(domain,range,status,iter,add,restart)
- The same idea as the forward function, this time for wrapping the
adjoint operation.
To build more complex operations there are two component operator classes
SEP.vector.chain and
SEP.vector.array.
Both of the complex operators are initialized by a string descriptor
and an array of operators.
The SEP.vector.chain chains
two operators, an example is the preconditioning
problem,
| 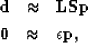 |
(2) |
| |
where 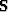 is the preconditioning operator and
is the preconditioning operator and 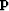 is
a vector in the domain of
is
a vector in the domain of 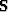 . In this
case SEP.vector.chain would be formed from
. In this
case SEP.vector.chain would be formed from
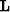 and
and 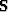 .A condition of forming this operator is that
the range vector of operator i must exist in
the same space as the domain vector of i+1. When this
operator is initialized it will automatically create all of the intermediate spaces.
The other class, SEP.vector.array creates a new operator
which is a matrix of existing operators. For examples we can think of the regularization
inverse problem in terms of the matrices,
.A condition of forming this operator is that
the range vector of operator i must exist in
the same space as the domain vector of i+1. When this
operator is initialized it will automatically create all of the intermediate spaces.
The other class, SEP.vector.array creates a new operator
which is a matrix of existing operators. For examples we can think of the regularization
inverse problem in terms of the matrices,
| 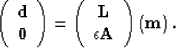 |
(3) |
The SEP.vector.array is initialized
by the array of operators and the number of collums
and rows in the new array operator.
In forming the operator the library makes sure that all of the domain
and range vectors make sense (for the regularization problem the
domain of 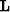 and
and 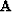 must be the same.
From these two building blocks any inverse problem can be described.
must be the same.
From these two building blocks any inverse problem can be described.





Next: Solver
Up: Abstract Classes
Previous: Vectors and super vectors
Stanford Exploration Project
10/23/2004