




Next: Modeling of the multiples
Up: Subtraction of multiples
Previous: Adaptive subtraction
As shown in Guitton (2003b), the estimated signal is
given by:
| 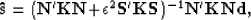 |
(3) |
where 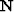 and
and 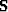 are the noise and signal prediction
error filters (PEFs), respectively,
are the noise and signal prediction
error filters (PEFs), respectively,  a trade-off parameter
and
a trade-off parameter
and 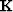 a masking operator. The noise PEFs are estimated from
the noise model. The signal PEFs are estimated with the Spitz
approximation Guitton (2004).
As we shall see later, the Spitz approximation works
very well when the noise and signal are uncorrelated.
3D filters are estimated since they lead to the best multiple
attenuation results
Guitton (2003a, 2004).
a masking operator. The noise PEFs are estimated from
the noise model. The signal PEFs are estimated with the Spitz
approximation Guitton (2004).
As we shall see later, the Spitz approximation works
very well when the noise and signal are uncorrelated.
3D filters are estimated since they lead to the best multiple
attenuation results
Guitton (2003a, 2004).
For the following results, the filters size is 15 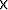 3
3 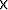 3
(the last number corresponds to the shot axis) and the patch
size is 16
3
(the last number corresponds to the shot axis) and the patch
size is 16 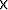 8
8 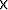 5. These numbers are identical for both
noise and signal filters. With 3D filters, because of memory limitations,
we cannot estimate the signal for a complete 2D line on one
computer only. Therefore, we segment the 2D
line into macro-patches of 50 successive shots. There is an overlap
of 5 shots between adjacent macro-patches. Each macro-patch is
processed on one node before being merged into the final file.
5. These numbers are identical for both
noise and signal filters. With 3D filters, because of memory limitations,
we cannot estimate the signal for a complete 2D line on one
computer only. Therefore, we segment the 2D
line into macro-patches of 50 successive shots. There is an overlap
of 5 shots between adjacent macro-patches. Each macro-patch is
processed on one node before being merged into the final file.





Next: Modeling of the multiples
Up: Subtraction of multiples
Previous: Adaptive subtraction
Stanford Exploration Project
5/23/2004
![]() 3
3 ![]() 3
(the last number corresponds to the shot axis) and the patch
size is 16
3
(the last number corresponds to the shot axis) and the patch
size is 16 ![]() 8
8 ![]() 5. These numbers are identical for both
noise and signal filters. With 3D filters, because of memory limitations,
we cannot estimate the signal for a complete 2D line on one
computer only. Therefore, we segment the 2D
line into macro-patches of 50 successive shots. There is an overlap
of 5 shots between adjacent macro-patches. Each macro-patch is
processed on one node before being merged into the final file.
5. These numbers are identical for both
noise and signal filters. With 3D filters, because of memory limitations,
we cannot estimate the signal for a complete 2D line on one
computer only. Therefore, we segment the 2D
line into macro-patches of 50 successive shots. There is an overlap
of 5 shots between adjacent macro-patches. Each macro-patch is
processed on one node before being merged into the final file.