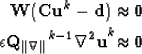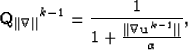Next: Real data Results
Up: ``Blocky'' Models
Previous: Edge preserving regularization with
In the previous section we changed the norm of the minimization problem to prevent the roughener from smoothing over the edges of the model. In this subsection we shift from a statistical to a more mechanical approach to attain the same goal.
To preserve the edges of the model Clapp et al. (1998) propose adding a weight to zero the model residual at the edges. Lizarralde and Swift (1999) implement a similar approach for the
inversion of VSP data for interval velocity. This approach requires human intervention for reflector picking.
We want to design a weight which de-weights edges in the model residual, but which is estimated automatically.
The 2-D gradient magnitude is a good isotropic edge-detection operator that can be used to calculate the diagonal weights. As we show in the deblurring problem Valenciano et al. (2003), using the gradient magnitude we can iteratively obtain sharp edges.
We perform the following non linear iterations: starting with 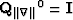 , at the kth iteration the algorithm solves
, at the kth iteration the algorithm solves
| 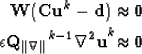 |
|
| (8) |
where
| 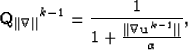 |
(9) |
and 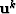 is the result of the kth nonlinear iteration,
is the result of the kth nonlinear iteration,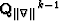 is the (k-1)th diagonal weight operator,
is the (k-1)th diagonal weight operator,  is the gradient magnitude,
is the gradient magnitude, 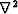 is the Laplacian operator,
is the Laplacian operator, 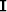 is the identity matrix, the scalar
is the identity matrix, the scalar  is the trade-off parameter controlling the discontinuities in the solution, and the scalar
is the trade-off parameter controlling the discontinuities in the solution, and the scalar  balances the relative importance of model and data residuals.
balances the relative importance of model and data residuals.





Next: Real data Results
Up: ``Blocky'' Models
Previous: Edge preserving regularization with
Stanford Exploration Project
10/14/2003
![]() , at the kth iteration the algorithm solves
, at the kth iteration the algorithm solves