




Next: Born wave-equation MVA
Up: Sava and Fomel: WEMVA
Previous: Introduction
In migration by downward-continuation, the wavefield at depth
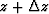 ,
, 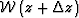 , is obtained by phase-shift from the wavefield at
depth z,
, is obtained by phase-shift from the wavefield at
depth z, 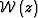 .
.
| 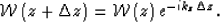 |
(1) |
This equation corresponds to the analytical solution of the ordinary
differential equation
| 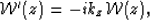 |
(2) |
where the ' sign represents a derivative with respect to the
depth z.
We can consider that the depth wavenumber (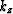 ) depends linearly,
through a Taylor series expansion, on its value in the reference
medium (
) depends linearly,
through a Taylor series expansion, on its value in the reference
medium (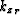 ) and the laterally varying slowness in the depth
interval from z to
) and the laterally varying slowness in the depth
interval from z to 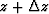 ,
, 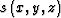
| 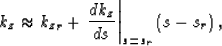 |
(3) |
where sr represents the constant slowness associated with the
depth slab between the two depth intervals, and 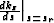 represents the
derivative of the depth wavenumber with respect to the reference
slowness and which can be implemented in many different ways
Sava (2000).
The wavefield downward-continued through the background slowness
represents the
derivative of the depth wavenumber with respect to the reference
slowness and which can be implemented in many different ways
Sava (2000).
The wavefield downward-continued through the background slowness
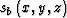 can, therefore, be written as
can, therefore, be written as
| ![\begin{displaymath}
\mathcal W_b \left({z+\Delta z} \right)=\mathcal W\left(z \r...
...d s} \right\vert _{s=s_r}\left(s_b- s_r\right)\right]\Delta z},\end{displaymath}](img12.gif) |
(4) |
from which we obtain that the full wavefield 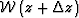 depends on the
background wavefield
depends on the
background wavefield 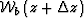 through the relation
through the relation
| 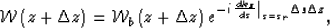 |
(5) |
where 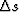 represents the difference between the
true and background slownesses
represents the difference between the
true and background slownesses 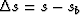 .
.





Next: Born wave-equation MVA
Up: Sava and Fomel: WEMVA
Previous: Introduction
Stanford Exploration Project
6/7/2002
![]() ) depends linearly,
through a Taylor series expansion, on its value in the reference
medium (
) depends linearly,
through a Taylor series expansion, on its value in the reference
medium (![]() ) and the laterally varying slowness in the depth
interval from z to
) and the laterally varying slowness in the depth
interval from z to ![]() ,
, ![]()