




Next: DOUBLE-POROSITY GEOMECHANICS
Up: Berryman: Double-porosity analysis
Previous: INTRODUCTION
In the absence of external driving forces that can
maintain fluid-pressure differentials over long time periods,
double-porosity and multi-porosity models must all reduce to
single-porosity models. This reduction occurs in the long-time
limit when the matrix fluid pressure and joint fluid
pressure become equal. It is therefore necessary to remind ourselves of the
basic results for single-porosity models in poroelasticity
(Biot 1941; Detournay and Cheng 1993; Wang 2000), as the
long-time behavior may be viewed as providing limiting
temporal boundary conditions (for 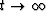 )on the analysis of multi-porosity coefficients.
Further, in the specific models we adopt for the
geomechanical constants in the multi-porosity theory, extensive use
of the single-porosity results will be made.
)on the analysis of multi-porosity coefficients.
Further, in the specific models we adopt for the
geomechanical constants in the multi-porosity theory, extensive use
of the single-porosity results will be made.
The volume changes of any isothermal, isotropic material
can only be created by hydrostatic pressure changes.
The two fundamental pressures of single-porosity poroelasticity
are the confining (external) pressure pc and the fluid (pore) pressure
pf. The differential pressure (or Terzaghi effective stress)
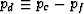 is often used
instead of the confining pressure. The volumetric response of a sample
due to small changes in pd and pf take the form
[e.g., Brown and Korringa (1975)]
is often used
instead of the confining pressure. The volumetric response of a sample
due to small changes in pd and pf take the form
[e.g., Brown and Korringa (1975)]
| 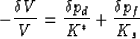 |
(2) |
for the total volume V,
| 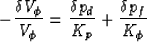 |
(3) |
for the pore volume 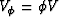 (where
(where 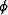 is the porosity), and
is the porosity), and
| 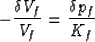 |
(4) |
for the fluid volume Vf.
Equation (totalV) serves to define the drained (or ``jacketed'')
frame bulk modulus K* and the unjacketed bulk modulus Ks for the composite frame. Equation (poreV) defines the jacketed
pore modulus Kp and the unjacketed pore modulus 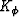 .Similarly, (fluidV) defines the bulk modulus Kf of the pore
fluid.
.Similarly, (fluidV) defines the bulk modulus Kf of the pore
fluid.
Treating 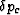 and
and 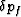 as the independent
variables, we define the dependent variables to be
as the independent
variables, we define the dependent variables to be
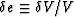 and
and 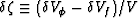 ,
which are termed
respectively the total volume dilatation (positive when a sample
expands) and the increment of fluid content (positive when the net
fluid mass flow is into the sample during deformation).
Then, it follows directly from these definitions and
from (totalV), (poreV), and (fluidV) that
,
which are termed
respectively the total volume dilatation (positive when a sample
expands) and the increment of fluid content (positive when the net
fluid mass flow is into the sample during deformation).
Then, it follows directly from these definitions and
from (totalV), (poreV), and (fluidV) that
| 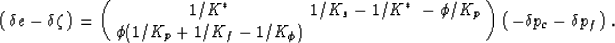 |
(5) |
Now we consider two well-known thought experiments: the drained test
and the undrained test
(Gassmann 1951; Biot and Willis 1957; Geertsma 1957; Wang, 2000).
In the drained test,the porous material is surrounded by an impermeable jacket and the
fluid is allowed to escape through a conduit penetrating the jacket.
Then, in a long duration experiment, the fluid pressure remains in
equilibrium with the external fluid pressure (e.g., atmospheric) and so
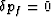 . Hence,
. Hence, 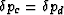 .So changes of total volume and pore
volume are given by the drained constants 1/K* and 1/Kp as defined
in (totalV) and (poreV). In contrast, for the undrained
test, the jacketed sample has no connection to the outside world, so pore
pressure responds only to the confining pressure changes. With no way
out, the total fluid content cannot change, so the increment
.So changes of total volume and pore
volume are given by the drained constants 1/K* and 1/Kp as defined
in (totalV) and (poreV). In contrast, for the undrained
test, the jacketed sample has no connection to the outside world, so pore
pressure responds only to the confining pressure changes. With no way
out, the total fluid content cannot change, so the increment 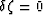 .Then, the second equation in (defs) shows that
.Then, the second equation in (defs) shows that
| 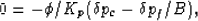 |
(6) |
where Skempton's pore pressure buildup coefficient B (Skempton 1954)
is defined by
| 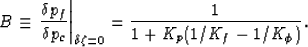 |
(7) |
It follows immediately from this definition that the undrained modulus Ku
is determined by [also see Carroll (1980)]
| 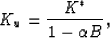 |
(8) |
where  is the combination of moduli known as the Biot-Willis
parameter, or the total volume effective-stress coefficient.
The precise definition of
is the combination of moduli known as the Biot-Willis
parameter, or the total volume effective-stress coefficient.
The precise definition of  follows immediately from the form of
(totalV), by substituting
follows immediately from the form of
(totalV), by substituting 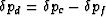 and rearranging the equation into the form
and rearranging the equation into the form
| 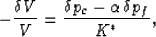 |
(9) |
with 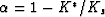 .The result (Gassmann) was apparently first obtained
by Gassmann (1951) (though not in this form) for the case of
microhomogeneous porous media (i.e.,
.The result (Gassmann) was apparently first obtained
by Gassmann (1951) (though not in this form) for the case of
microhomogeneous porous media (i.e., 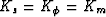 , the
bulk modulus of the single mineral present) and by Brown and Korringa (1975)
and Rice (1975) for general porous media with multiple minerals as
constituents. We will sometimes use the term ``Gassmann material''
when making reference to a microhomogeneous porous medium.
, the
bulk modulus of the single mineral present) and by Brown and Korringa (1975)
and Rice (1975) for general porous media with multiple minerals as
constituents. We will sometimes use the term ``Gassmann material''
when making reference to a microhomogeneous porous medium.
Next, to clarify the structure of (defs) further, note that
Betti's reciprocal theorem (Love 1927), shows that
the drained and undrained pressures and strains satisfy a
reciprocal relation, from which it follows that
| 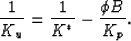 |
(10) |
Comparing (Gassmann) with (reciprBetti), we
obtain the general reciprocity relation (Brown and Korringa 1975)
| 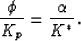 |
(11) |
This reciprocity relation and the form of the
compressibility laws (defs) also follow directly from
general thermodynamic arguments [e.g., Pride and Berryman (1998)].
Then, Skempton's pore-pressure buildup coefficient (Skempton 1954)
may be written alternatively as
| 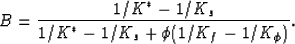 |
(12) |
Finally, the condensed form of (defs) --
incorporating the reciprocity relations --
is
| 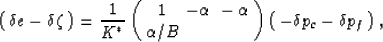 |
(13) |
where the Biot-Willis (1957) parameter  can now be expressed as
can now be expressed as
| 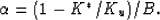 |
(14) |
The parameter  is also known as the total volume
effective-stress coefficient [see Berryman (1992) for elaboration].
This form of the compressibility laws is especially convenient
because all the coefficients are simply related to the three moduli
K*, Ku, and B that have the clearest physical interpretations.
This now completes our review of the standard
results concerning the single-porosity compressibility laws.
is also known as the total volume
effective-stress coefficient [see Berryman (1992) for elaboration].
This form of the compressibility laws is especially convenient
because all the coefficients are simply related to the three moduli
K*, Ku, and B that have the clearest physical interpretations.
This now completes our review of the standard
results concerning the single-porosity compressibility laws.





Next: DOUBLE-POROSITY GEOMECHANICS
Up: Berryman: Double-porosity analysis
Previous: INTRODUCTION
Stanford Exploration Project
6/8/2002
![]() )on the analysis of multi-porosity coefficients.
Further, in the specific models we adopt for the
geomechanical constants in the multi-porosity theory, extensive use
of the single-porosity results will be made.
)on the analysis of multi-porosity coefficients.
Further, in the specific models we adopt for the
geomechanical constants in the multi-porosity theory, extensive use
of the single-porosity results will be made.
![]() is often used
instead of the confining pressure. The volumetric response of a sample
due to small changes in pd and pf take the form
[e.g., Brown and Korringa (1975)]
is often used
instead of the confining pressure. The volumetric response of a sample
due to small changes in pd and pf take the form
[e.g., Brown and Korringa (1975)]
![]() and
and ![]() as the independent
variables, we define the dependent variables to be
as the independent
variables, we define the dependent variables to be
![]() and
and ![]() ,
which are termed
respectively the total volume dilatation (positive when a sample
expands) and the increment of fluid content (positive when the net
fluid mass flow is into the sample during deformation).
Then, it follows directly from these definitions and
from (totalV), (poreV), and (fluidV) that
,
which are termed
respectively the total volume dilatation (positive when a sample
expands) and the increment of fluid content (positive when the net
fluid mass flow is into the sample during deformation).
Then, it follows directly from these definitions and
from (totalV), (poreV), and (fluidV) that
![]() . Hence,
. Hence, ![]() .So changes of total volume and pore
volume are given by the drained constants 1/K* and 1/Kp as defined
in (totalV) and (poreV). In contrast, for the undrained
test, the jacketed sample has no connection to the outside world, so pore
pressure responds only to the confining pressure changes. With no way
out, the total fluid content cannot change, so the increment
.So changes of total volume and pore
volume are given by the drained constants 1/K* and 1/Kp as defined
in (totalV) and (poreV). In contrast, for the undrained
test, the jacketed sample has no connection to the outside world, so pore
pressure responds only to the confining pressure changes. With no way
out, the total fluid content cannot change, so the increment ![]() .Then, the second equation in (defs) shows that
.Then, the second equation in (defs) shows that