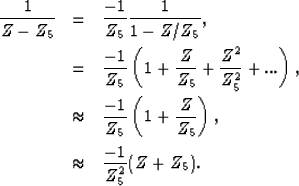Next: Conclusion
Up: Stability of the Hessian
Previous: The Spitz estimate
Now I consider the Z-transforms of the data, signal and noise PEFs for a
1D case. For the data PEF  , I assume that the filter has the form
, I assume that the filter has the form
| 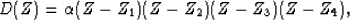 |
(9) |
with 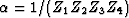 . The Zi correspond to the roots of
the filter.
In this example I consider that Z1 and Z2 are the roots
for the noise and Z3 and Z4 the roots for the signal.
Now I assume that we have for the noise
PEF
. The Zi correspond to the roots of
the filter.
In this example I consider that Z1 and Z2 are the roots
for the noise and Z3 and Z4 the roots for the signal.
Now I assume that we have for the noise
PEF 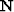
| 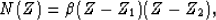 |
(10) |
with 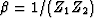 . The Spitz estimate yields for the signal PEF
. The Spitz estimate yields for the signal PEF 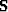
| 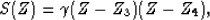 |
(11) |
with 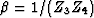 . We see that by construction, the signal and
noise PEF annihilate different parts of the data space and can't overlap.
. We see that by construction, the signal and
noise PEF annihilate different parts of the data space and can't overlap.
Now, If we assume that the noise PEF is a ``bad'' estimate of the noise with
one erroneous root, i.e,
| 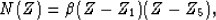 |
(12) |
with 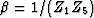 , we find for the signal PEF
, we find for the signal PEF 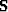
| 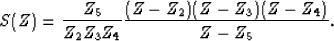 |
(13) |
Because the PEFs are minimum phase, we can write
| 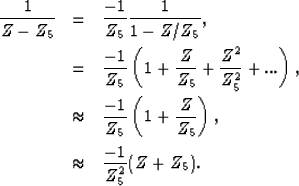 |
|
| |
| (14) |
| |
Then we obtain for the signal PEF
| 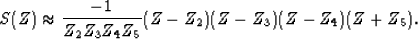 |
(15) |
The wrong root in the noise PEF leaks in the signal PEF but with an
opposite sign. Again, the Spitz estimate makes it impossible for
the signal and noise operators to overlap in the data space.
This simple example in 1D can be easily expendable in 2D via
the helical coordinates Claerbout (1998).





Next: Conclusion
Up: Stability of the Hessian
Previous: The Spitz estimate
Stanford Exploration Project
6/7/2002