|
|
|
|
Fast log-decon with a quasi-Newton solver |
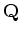 .
This technique is very cost effective: given the most recent history of
gradient and model vectors (usually around 5) kept in memory, the quasi-Newton
search direction
.
This technique is very cost effective: given the most recent history of
gradient and model vectors (usually around 5) kept in memory, the quasi-Newton
search direction
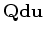 (inverse Hessian times the gradient) is
computed directly with simple vector multiplications. Therefore, the L-BFGS solver
can be used for large non-linear problems (Nocedal, 1980).
(inverse Hessian times the gradient) is
computed directly with simple vector multiplications. Therefore, the L-BFGS solver
can be used for large non-linear problems (Nocedal, 1980).
Contrary to steepest descent where the step length is estimated with a Newton-search technique, the step length in L-BFGS is computed such that sufficient decrease of the error and of the local curvature is attained (so called ``Wolfe conditions''). The appendix shows the L-BFGS solver in more details. The L-BFGS code can be downloaded at http://users.eecs.northwestern.edu/~nocedal/lbfgs.html The pseudo-code below shows both the steepest-descent and L-BFGS algorithms.
U = 0. # or other initializations
Remove the mean from U(omega).
Iteration {
dU = 0
Compute dU
Remove mean from dU
du = FT(dU)
if (steepest descent)
{
Compute alfa with Newton iterations
u = u + alfa*du
}
else if (L-BFGS)
{
Compute alfa with More and Thuente method
u = u + alfa*Qdu # Q = inverse approximate Hessian
}
}