




Next: Unit circle
Up: Convolution and Spectra
Previous: Fourier sum
The frequency function of a pulse at time
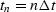 is
is
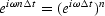 .The factor
.The factor 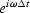 occurs so often in applied work
that it has a name:
occurs so often in applied work
that it has a name:
| 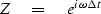 |
(20) |
With this Z, the pulse at time tn is compactly represented as Zn.
The variable Z makes
Fourier transforms
look like polynomials,
the subject of a literature called
``Z-transforms.''
The Z-transform is a variant form of the Fourier transform
that is particularly useful for time-discretized (sampled) functions.
From the definition (20), we have
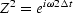 ,
,
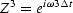 ,etc.
Using these equivalencies,
equation (19) becomes
,etc.
Using these equivalencies,
equation (19) becomes
| 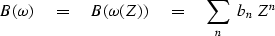 |
(21) |





Next: Unit circle
Up: Convolution and Spectra
Previous: Fourier sum
Stanford Exploration Project
3/1/2001
![]() is
is
![]() .The factor
.The factor ![]() occurs so often in applied work
that it has a name:
occurs so often in applied work
that it has a name:
![]() ,
,
![]() ,etc.
Using these equivalencies,
equation (19) becomes
,etc.
Using these equivalencies,
equation (19) becomes