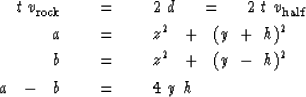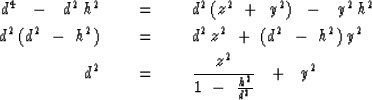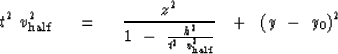The migration ellipse

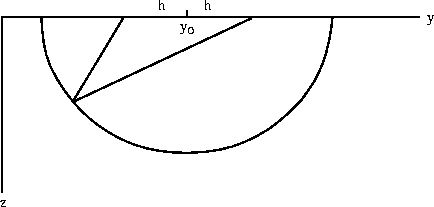
Another insight into equation (5) is to regard the offset h and the total travel time t as fixed constants. Then the locus of possible reflectors turns out to describe an ellipse in the plane of (y-y₀ ,z). The reason it is an ellipse follows from the geometric definition of an ellipse. To draw an ellipse, place a nail or tack into s on Figure 17 and another into g. Connect the tacks by a string that is exactly long enough to go through (y₀ ,z). An ellipse going through (y₀ ,z) may be constructed by sliding a pencil along the string, keeping the string tight. The string keeps the total distance tv constant.

Recall that one method for migrating zero-offset sections is to take every data value in (y,t)-space and use it to superpose an appropriate semicircle in (y,z)-space. For nonzero offset the circle should be generalized to an ellipse (Figure ).

It is not easy to show that equation (5) can be cast in the standard mathematical form of an ellipse, namely, a stretched circle. But the result is a simple one, and an important one for later analysis, so here we go. Equation (5) in (y,h)-space is  

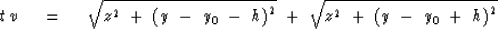$$t\,v\ \eq \ \sqrt { z^2\ +\ {( y \ -\ y_0 \ - \ h) }^2} \ +\ \sqrt { z^2\ +\ {( y \ -\ y_0 \ + \ h) }^2}$$ (9)

To help reduce algebraic verbosity, define a new y equal to the old one shifted by y₀. Also make the definitions

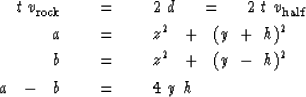$$\begin{eqnarray} t\,v_{\rm rock} \ \ \ \ &=&\ \ \ \ 2\ d\ \eq \ 2\ t\ v_{\rm hal... ... z^2 \ \ +\ \ (y\ -\ h)^2 \\ a\ \ -\ \ b\ \ \ \ &=&\ \ \ \ 4\ y\ h\end{eqnarray}$$ (10) (11) (12) (13)

With these definitions, (9) becomes  

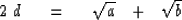$$2\ d\ \eq \ \sqrt a \ \ +\ \ \sqrt b$$ (14)

Square to get a new equation with only one square root.  

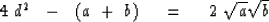$$4\ d^2 \ \ -\ \ (a\ +\ b) \ \eq \ 2\ \sqrt a \sqrt b$$ (15)

Square again to eliminate the square root.

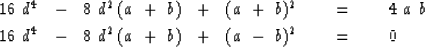$$\begin{eqnarray} 16\ d^4 \ \ -\ \ 8\ d^2 \, (a\ +\ b) \ \ +\ \ (a\ +\ b)^2 \ \ \... ...\ \ 8\ d^2 \, (a\ +\ b) \ \ +\ \ (a\ -\ b)^2 \ \ \ \ &=& \ \ \ \ 0\end{eqnarray}$$ (16) (17)

Introduce definitions of a and b.  

$$16\ d^4 \ \ -\ \ 8\ d^2 \ [\,2\,z^2 \ +\ 2\,y^2 \ +\ 2\,h^2 ] \ \ +\ \ 16\ y^2 \, h^2 \ \eq \ 0$$ (18)

Bring y and z to the right.

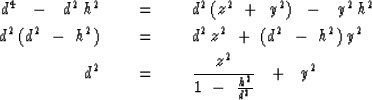$$\begin{eqnarray} d^4 \ \ -\ \ d^2 \, h^2 \ \ \ \ &=&\ \ \ \ d^2 \, ( z^2 \ +\ y... ... \ \ \ \ &=&\ \ \ \ {z^2 \over 1 \ -\ {h^2 \over d^2}}\ \ +\ \ y^2\end{eqnarray}$$ (19) (20) (21)

Finally, recalling all earlier definitions,  

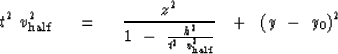$$t^2 \ v_{\rm half}^2 \ \eq \ {z^2 \over 1 \ -\ {h^2 \over t^2 \ v_{\rm half}^2}} \ \ +\ \ (y\ -\ y_0 )^2$$ (22)

Fixing t, equation (22) is the equation for a circle with a stretched z-axis. Our algebra has confirmed that the ``string and tack'' definition of an ellipse matches the ``stretched circle'' definition. An ellipse in model space is the earth model given the observation of an impulse on a constant-offset section.

 

ellipse
Figure 23 Migration ellipse.

 

shell
Figure 24 Undocumented data from a recruitment brochure. This data may be assumed to be of textbook quality. The speed of sound in water is about 1500 m/sec. Identify the events at A, B, and C. Is this a common-shotpoint gather or a common-midpoint gather? (Shell Oil Company)