




Next: Stability of the differential
Up: The craft of wavefield
Previous: Fractional integration and constant
Stable extrapolation can be assured by preserving certain symmetries.
It will be shown that stability is
assured in both the differential equation
| 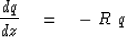 |
(80) |
and its Crank-Nicolson approximation
| 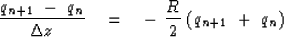 |
(81) |
provided that 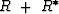 is
a positive definite (actually, semidefinite) matrix.
When stability was studied in the previous section
the operator R was a scalar Z-transform.
Because Z-transforms were used,
the mathematics of that section was particularly suitable
for time domain migrations.
Because R was a scalar,
the mathematics of that section was particularly suitable
when data has been Fourier transformed over x.
Here we will focus on the
matrix
character of R.
Thus we are concerning ourselves with migration in the x-domain.
Our purpose in doing this theoretical work
is to gain the ability to write a ``bulletproof'' program
for migrating seismic data in the presence of lateral velocity variation.
As an example,
the familiar 45
is
a positive definite (actually, semidefinite) matrix.
When stability was studied in the previous section
the operator R was a scalar Z-transform.
Because Z-transforms were used,
the mathematics of that section was particularly suitable
for time domain migrations.
Because R was a scalar,
the mathematics of that section was particularly suitable
when data has been Fourier transformed over x.
Here we will focus on the
matrix
character of R.
Thus we are concerning ourselves with migration in the x-domain.
Our purpose in doing this theoretical work
is to gain the ability to write a ``bulletproof'' program
for migrating seismic data in the presence of lateral velocity variation.
As an example,
the familiar 45 extrapolation equation
will be put in the bulletproof form.
This section, combined with the previous one,
gives a general theory for stable migration in (t,x)-space.
extrapolation equation
will be put in the bulletproof form.
This section, combined with the previous one,
gives a general theory for stable migration in (t,x)-space.





Next: Stability of the differential
Up: The craft of wavefield
Previous: Fractional integration and constant
Stanford Exploration Project
10/31/1997