




Next: The unit circle
Up: INSTABILITY
Previous: Anticausality
Let bt denote a filter.
Then at is its ``inverse filter''
if the convolution of at with bt is an impulse function.
Filters are said to be inverse to one another if their Fourier transforms
are inverse to one another.
So in terms of Z-transforms,
the filter A(Z) is said to be inverse to the signal of B(Z)
if A(Z)B(Z)=1.
What we have seen so far is that the inverse filter can be stable
or unstable depending on the location of its poles.
Likewise, if B(Z) is a filter, then A(Z) is a usable filter
inverse to B(Z), if A(Z)B(Z)=1 and if A(Z) does not have coefficients
that tend to infinity.
Another approach to inverse filters lies in the Fourier domain.
There a filter inverse to bt is the at made by taking the
inverse Fourier
transform of 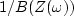 .If B(Z) has its zeros outside the unit circle,
then at will be causal; otherwise not.
In the Fourier domain the only danger is dividing by a zero,
which would be a pole on the unit circle.
In the case of Z-transforms,
zeros should not only be off the circle
but also outside it.
So the
.If B(Z) has its zeros outside the unit circle,
then at will be causal; otherwise not.
In the Fourier domain the only danger is dividing by a zero,
which would be a pole on the unit circle.
In the case of Z-transforms,
zeros should not only be off the circle
but also outside it.
So the  -domain seems safer than the Z-domain.
Why not always use the Fourier domain?
The reasons we do not always inverse filter in the
-domain seems safer than the Z-domain.
Why not always use the Fourier domain?
The reasons we do not always inverse filter in the
 -domain, along with many illustrations,
are given in chapter
-domain, along with many illustrations,
are given in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.





Next: The unit circle
Up: INSTABILITY
Previous: Anticausality
Stanford Exploration Project
10/21/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![]() .If B(Z) has its zeros outside the unit circle,
then at will be causal; otherwise not.
In the Fourier domain the only danger is dividing by a zero,
which would be a pole on the unit circle.
In the case of Z-transforms,
zeros should not only be off the circle
but also outside it.
So the
.If B(Z) has its zeros outside the unit circle,
then at will be causal; otherwise not.
In the Fourier domain the only danger is dividing by a zero,
which would be a pole on the unit circle.
In the case of Z-transforms,
zeros should not only be off the circle
but also outside it.
So the ![]() -domain seems safer than the Z-domain.
Why not always use the Fourier domain?
The reasons we do not always inverse filter in the
-domain seems safer than the Z-domain.
Why not always use the Fourier domain?
The reasons we do not always inverse filter in the
![]() -domain, along with many illustrations,
are given in chapter
-domain, along with many illustrations,
are given in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.