




Next: Plots
Up: Z-plane, causality, and feedback
Previous: Z-plane, causality, and feedback
The convolution equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
)
| 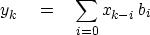 |
(2) |
says that the present output is created entirely from present
and past values of the input.
Now we will include past values of the output.
The simplest example is
numerical integration,
such as
| 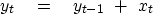 |
(3) |
Notice that when 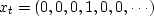 ,
,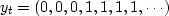 ,which shows that the integral of an impulse is a step.
,which shows that the integral of an impulse is a step.
A kind of deliberately imperfect integration used in numerical work
is called ``leaky integration.''
The name derives from the analogous situation of
electrical circuits, where
the voltage on a capacitor is the integral of the current:
in real life, some of the current leaks away.
An equation to model leaky integration is
| 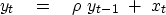 |
(4) |
where 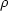 is a constant that is slightly less than plus one.
Notice that if
is a constant that is slightly less than plus one.
Notice that if 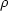 were greater than unity,
the output of (4) would grow with time instead of decaying.
A program for this simple operation is leak().
I use this program so frequently
that I wrote it so the output could be overlaid on the input.
leak() uses a trivial subroutine, copy()
were greater than unity,
the output of (4) would grow with time instead of decaying.
A program for this simple operation is leak().
I use this program so frequently
that I wrote it so the output could be overlaid on the input.
leak() uses a trivial subroutine, copy() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , for copying.
, for copying.
subroutine leak( rho, n, xx, yy)
integer i, n; real xx(n), yy(n), rho
temporary real tt( n)
call null( tt, n)
tt(1) = xx(1)
do i= 2, n
tt(i) = rho * tt(i-1) + xx(i)
call copy( n, tt, yy)
return; end
Let us see what Z-transform equation is implied by (4).
Move the y terms to the left:
| 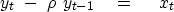 |
(5) |
Given the Z-transform equation
| 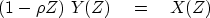 |
(6) |
notice that (5) can be derived
from (6)
by finding the
coefficient of Zt.
Thus we can say that the output Y(Z) is derived from the input X(Z) by
the polynomial division
| 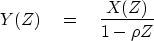 |
(7) |
Therefore, the effective filter B(Z) in Y(Z)=B(Z)X(Z) is
| 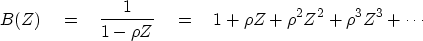 |
(8) |
The left side of Figure 1 shows a damped exponential
function that consists of the coefficients 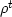 seen in
equation (8).
leak
seen in
equation (8).
leak
Figure 1
Left is the impulse response of leaky integration.
Right is the amplitude 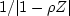 in the Fourier domain.
in the Fourier domain.

The spectrum of bt is defined by 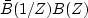 .The amplitude spectrum is the square root of the spectrum.
.The amplitude spectrum is the square root of the spectrum.
It can be abbreviated by |B(Z)|.
The amplitude spectrum is plotted on the right side of Figure 1.
Ordinary integration has a Fourier response 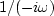 that blows up at
that blows up at 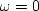 .Leaky integration smooths off
the infinite value at
.Leaky integration smooths off
the infinite value at 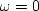 .Thus in the figure, the amplitude spectrum looks like
.Thus in the figure, the amplitude spectrum looks like 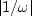 ,except that it is not
,except that it is not 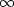 at
at 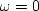 .
.





Next: Plots
Up: Z-plane, causality, and feedback
Previous: Z-plane, causality, and feedback
Stanford Exploration Project
10/21/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , for copying.
, for copying. 
![]() .The amplitude spectrum is the square root of the spectrum.
.The amplitude spectrum is the square root of the spectrum.
![]() that blows up at
that blows up at ![]() .Leaky integration smooths off
the infinite value at
.Leaky integration smooths off
the infinite value at ![]() .Thus in the figure, the amplitude spectrum looks like
.Thus in the figure, the amplitude spectrum looks like ![]() ,except that it is not
,except that it is not ![]() at
at ![]() .
.