




Next: Moving windows for nonstationarity
Up: DIP PICKING WITHOUT DIP
Previous: DIP PICKING WITHOUT DIP
A plane wave in a wave field u(t,x)=u(t-px) with stepout p
can be extinguished with a partial differential operator,
which we write as a matrix 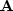 , where
, where
| 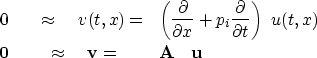 |
(25) |
| (26) |
The parameter p is called the ``wavenumber" or ``Snell parameter,"
and |p| can take on any value less than 1/v,
where v is the medium velocity.
The angle of propagation of the wave is 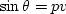 .
.
We need a method of discretization
that allows the mesh for du/dt to overlay exactly du/dx.
To this end
I chose to represent
the t-derivative by
| 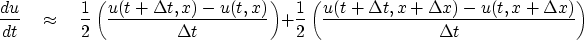 |
(27) |
and the x-derivative by an analogous expression
with t and x interchanged.
Now the difference operator 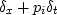 is a two-dimensional filter
that fits on a
is a two-dimensional filter
that fits on a  differencing star.
As a matrix operation,
this two-dimensional convolution is denoted
differencing star.
As a matrix operation,
this two-dimensional convolution is denoted  .(More details about finite differencing can be found in IEI.)
.(More details about finite differencing can be found in IEI.)
The program wavekill1() applies the operator
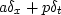 ,which can be specialized to the operators
,which can be specialized to the operators
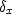 ,
,
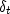 ,
,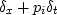 .
.
# vv = (aa Dx + pp Dt) uu
#
subroutine wavekill1( aa, pp, n1,n2,uu, vv )
integer i1,i2, n1,n2
real aa, pp, s11, s12, s21, s22, uu(n1,n2), vv( n1-1, n2-1)
s11 = -aa-pp; s12 = aa-pp
s21 = -aa+pp; s22 = aa+pp
call null( vv,(n1-1)*(n2-1))
do i1= 1, n1-1 { # vv is one point shorter than uu on both axes.
do i2= 1, n2-1 {
vv(i1,i2) = vv(i1,i2) +
uu(i1 ,i2) * s11 + uu(i1 ,i2+1) * s12 +
uu(i1+1,i2) * s21 + uu(i1+1,i2+1) * s22
}}
return; end
I carefully arranged the side boundaries so that the filter never
runs off the sides of the data.
Thus the output is shorter than the input by one point on
both the t-axis and the x-axis.
The reason for using these side boundaries is that large datasets
can be chopped into independent sections
without the boundaries themselves
affecting the result.
By chopping a large dataset into sections,
we can handle curved events as piecewise linear.
When only one wave is present and the data is adequately sampled,
then finding the best value of p is a single-parameter,
linear least-squares problem.
Let  be an abstract vector whose components are values of
be an abstract vector whose components are values of
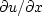 taken on a mesh in (t,x).
Likewise, let
taken on a mesh in (t,x).
Likewise, let 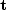 contain
contain 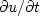 .Since we want
.Since we want 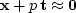 ,we minimize the quadratic function of p,
,we minimize the quadratic function of p,
| 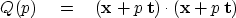 |
(28) |
by setting to zero the derivative. We get
| 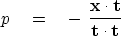 |
(29) |
Since data will not always fit the model very well,
it may be helpful to have some
way to measure how good the fit is.
I suggest
| 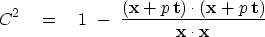 |
(30) |
which,
on inserting 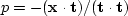 ,leads to C,
where
,leads to C,
where
| 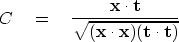 |
(31) |
is known as the ``normalized correlation.''
The program for this calculation is straightforward.
I named the program puck() to denote
picking on a continuum.
# measure coherency and dip, and compute residual res = (Dx + p Dt) uu
#
subroutine puck ( n1, n2, uu, coh, pp, res )
integer i1, i2, n1, n2
real uu(n1,n2), res(n1,n2), xx, xt, tt, coh, pp
temporary real dx(n1,n2-1), dt(n1-1,n2-1)
call wavekill1( 1., 0., n1,n2 , uu, dx)
call wavekill1( 0., 1., n1,n2 , uu, dt)
xx = 1.e-30; tt = 1.e-30; xt = 0.
do i1= 1, n1-1 {
do i2= 1, n2-1 {
xt = xt + dt(i1,i2) * dx(i1,i2)
tt = tt + dt(i1,i2) * dt(i1,i2)
xx = xx + dx(i1,i2) * dx(i1,i2)
}}
coh = sqrt((xt/tt)*(xt/xx))
pp = - xt/tt
call wavekill1( 1., pp, n1,n2 , uu, res)
return; end
Finally and parenthetically,
an undesirable feature of the
plane-wave destructor method
is that the residual  has no particular relation to the data
has no particular relation to the data 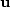 ,unlike in time-series analysis--see chapter
,unlike in time-series analysis--see chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Another disadvantage, well known to people who routinely work
with finite-difference solutions to partial differential equations,
is that for short wavelengths
a difference operator is not the same as a differential operator;
thereby the numerical value of p is biased.
.
Another disadvantage, well known to people who routinely work
with finite-difference solutions to partial differential equations,
is that for short wavelengths
a difference operator is not the same as a differential operator;
thereby the numerical value of p is biased.





Next: Moving windows for nonstationarity
Up: DIP PICKING WITHOUT DIP
Previous: DIP PICKING WITHOUT DIP
Stanford Exploration Project
10/21/1998
![]() , where
, where
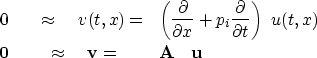
![]() ,which can be specialized to the operators
,which can be specialized to the operators
![]() ,
,
![]() ,
,![]() .
. ![]() be an abstract vector whose components are values of
be an abstract vector whose components are values of
![]() taken on a mesh in (t,x).
Likewise, let
taken on a mesh in (t,x).
Likewise, let ![]() contain
contain ![]() .Since we want
.Since we want ![]() ,we minimize the quadratic function of p,
,we minimize the quadratic function of p,
![]() has no particular relation to the data
has no particular relation to the data ![]() ,unlike in time-series analysis--see chapter
,unlike in time-series analysis--see chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Another disadvantage, well known to people who routinely work
with finite-difference solutions to partial differential equations,
is that for short wavelengths
a difference operator is not the same as a differential operator;
thereby the numerical value of p is biased.
.
Another disadvantage, well known to people who routinely work
with finite-difference solutions to partial differential equations,
is that for short wavelengths
a difference operator is not the same as a differential operator;
thereby the numerical value of p is biased.