




Next: PHASE OF A MINIMUM-PHASE
Up: PHASE DELAY AND GROUP
Previous: Observation of dispersive waves
We have already discussed
(page ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
all-pass filters, i.e.,
filters with constant unit spectra.
They can be written as
)
all-pass filters, i.e.,
filters with constant unit spectra.
They can be written as
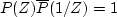 .In the frequency domain, P(Z)
can be expressed as
.In the frequency domain, P(Z)
can be expressed as 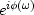 , where
, where
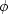 is real and is called the ``phase shift."
Clearly,
is real and is called the ``phase shift."
Clearly, 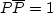 for all real
for all real 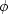 .It is an easy matter to make a filter
with any desired phase shift--we
merely Fourier transform
.It is an easy matter to make a filter
with any desired phase shift--we
merely Fourier transform
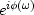 into the time domain.
If
into the time domain.
If 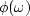 is arbitrary,
the resulting time function is likely to be two-sided.
Since we are interested in physical processes that are causal,
we may wonder what class of functions
is arbitrary,
the resulting time function is likely to be two-sided.
Since we are interested in physical processes that are causal,
we may wonder what class of functions
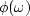 corresponds to one-sided time functions.
The answer is that the group delay
corresponds to one-sided time functions.
The answer is that the group delay
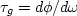 of a causal all-pass filter must be positive.
of a causal all-pass filter must be positive.
Proof that 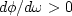 for a causal all-pass filter
is found in FGDP;
there is no need to reproduce the algebra here.
The proof begins from equation (
for a causal all-pass filter
is found in FGDP;
there is no need to reproduce the algebra here.
The proof begins from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and uses the imaginary part of the logarithm to get phase.
Differentiation with respect to
)
and uses the imaginary part of the logarithm to get phase.
Differentiation with respect to  yields a form
that is recognizable as a spectrum and hence is always positive.
yields a form
that is recognizable as a spectrum and hence is always positive.
A single-pole, single-zero all-pass filter
passes all frequency components with constant gain
and a phase shift that can be adjusted
by the placement of the pole.
Taking Z0 near the unit circle
causes most of the phase shift to be concentrated
near the frequency where the pole is located.
Taking the pole farther away causes the delay to be
spread over more frequencies.
Complicated phase shifts or group delays can be built up
by cascading single-pole filters.
The above reasoning for a single-pole, single-zero all-pass filter
also applies to many roots,
because the phase of each will add, and
the sum of 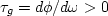 will be greater than zero.
will be greater than zero.
The Fourier dual to the positive group delay of a causal all-pass filter
is that the instantaneous frequency of a certain class of analytic
signals must be positive.
This class of analytic signals is made up of
all those with a constant envelope function,
as might be approximated by field data
after the process of automatic gain control.
EXERCISES:
-
Let xt be some real signal.
Let yt =xt+3
be another real signal.
Sketch the phase as a function of frequency
of the cross-spectrum X(1/Z)Y(Z) as
would a computer that put all arctangents in the principal
quadrants
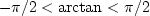 .Label the axis scales.
.Label the axis scales.
-
Sketch the amplitude, phase, and group delay of the all-pass filter
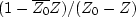 ,where
,where 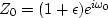 and
and
 is small.
Label important parameters on the curve.
is small.
Label important parameters on the curve.
-
Show that the coefficients of an all-pass,
phase-shifting filter made by cascading
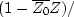 (Z0 - Z) with
(Z0 - Z) with
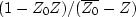 are real.
are real.
-
A continuous signal is the impulse
response of a continuous-time, all-pass filter.
Describe the function in both time and
frequency domains.
Interchange the words ``time"
and ``frequency" in your description of the function.
What is a physical example of such a function?
What happens to the statement,
the group delay of an all-pass filter is positive?
-
A graph of the group delay
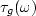 shows
shows  to be positive for all
to be positive for all  .What is the area under
.What is the area under
 in the range
in the range  ?
(HINT: This is a trick question you can solve
in your head.)
?
(HINT: This is a trick question you can solve
in your head.)





Next: PHASE OF A MINIMUM-PHASE
Up: PHASE DELAY AND GROUP
Previous: Observation of dispersive waves
Stanford Exploration Project
10/21/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and uses the imaginary part of the logarithm to get phase.
Differentiation with respect to
)
and uses the imaginary part of the logarithm to get phase.
Differentiation with respect to ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
all-pass filters, i.e.,
filters with constant unit spectra.
They can be written as
)
all-pass filters, i.e.,
filters with constant unit spectra.
They can be written as
![]() for a causal all-pass filter
is found in FGDP;
there is no need to reproduce the algebra here.
The proof begins from equation (
for a causal all-pass filter
is found in FGDP;
there is no need to reproduce the algebra here.
The proof begins from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and uses the imaginary part of the logarithm to get phase.
Differentiation with respect to
)
and uses the imaginary part of the logarithm to get phase.
Differentiation with respect to ![]() yields a form
that is recognizable as a spectrum and hence is always positive.
yields a form
that is recognizable as a spectrum and hence is always positive.
![]() will be greater than zero.
will be greater than zero.