The covariance matrix of multiple signals

A useful model of single-channel time-series analysis is that random numbers x_t enter a filter f_t and come out as a signal y_t.

A useful model of multiple-channel time-series analysis--with two channels, for example--is to start with independent random numbers in both the x₁(t) channel and the x₂(t) channel. Then we need four filters, f₁₁(t), f₁₂(t), f₂₁(t), and f₂₂(t), which produce two output signals defined by the Z-transforms

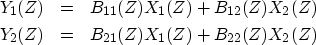$$\begin{eqnarray} Y_1(Z) &=& B_{11}(Z)X_1(Z) + B_{12}(Z)X_2(Z) \ Y_2(Z) &=& B_{21}(Z)X_1(Z) + B_{22}(Z)X_2(Z)\end{eqnarray}$$ (53) (54)

These signals have realistic characteristics. Each has its own spectral color. Each has a partial relationship to the other which is characterized by a spectral amplitude and phase. Typically we begin by examining the covariance matrix. For example, consider two time series, y₁(t) and y₂(t). Their Z-transforms are Y₁(Z) and Y₂(Z). Their covariance matrix is  

$$\left[ \begin{array} {cc} \E[ \overline{Y_1}(1/Z) Y_1(Z)]... ...egin{array} {cc} Y_1(Z) & Y_2(Z) \end{array} \right] \right)$$ (55)

Here Z-transforms represent the components of the matrix in the frequency domain. In the time domain, each of the four elements in the matrix of (55) becomes a Toeplitz matrix, a matrix of correlation functions (see page ).

The expectations in equation (55) are specified by theoretical assertions or estimated by sample averages or some combination of the two. Analogously to spectral factorization, the covariance matrix can be factored into two parts, 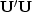$\bold U'\bold U$,where 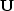$\bold U$ is an upper triangular matrix. The factorization might be done by the well known Cholesky method. The factorization is a multichannel generalization of spectral factorization and raises interesting questions about minimum-phase that are partly addressed in FGDP.