Bandlimited noise

Figure 5 shows bursts of 25 random numbers at various shifts, and their Fourier transforms. You can think of either side of the figure as the time domain and the other side as the frequency domain. (See page  for a description of the different ways of interpreting plots of one side of Fourier-transform pairs of even functions.) I like to think of the left side as the Fourier domain and the right side as the signals. Then the signals seem to be sinusoids of a constant frequency (called the ``center" frequency) and of an amplitude that is modulated at a slower rate (called the ``beat'' frequency). Observe that the center frequency is related to the location of the random bursts, and that the beat frequency is related to the bandwidth of the noise burst.

 

shift
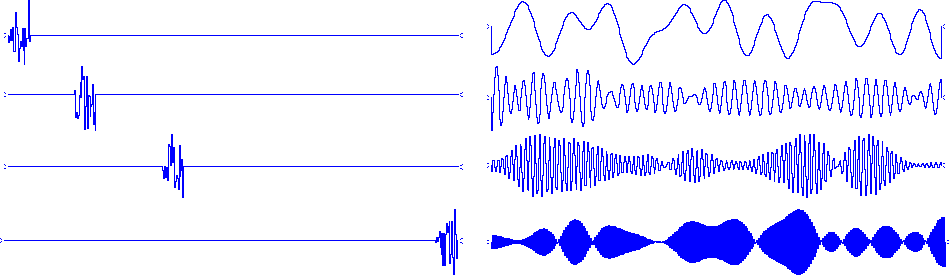
Figure 5 Shifted, zero-padded random numbers in bursts of 25 numbers. 1

You can also think of Figure 5 as having one-sided frequency functions on the left, and the right side as being the real part of the signal. The real parts are cosinelike, whereas the imaginary parts (not shown) are sinelike and have the same envelope function as the cosinelike part.

You might have noticed that the bottom plot in Figure 5, which has Nyquist-frequency modulated beats, seems to have about twice as many beats as the two plots above it. This can be explained as an end effect. The noise burst near the Nyquist frequency is really twice as wide as shown, because it is mirrored about the Nyquist frequency into negative frequencies. Likewise, the top figure is not modulated at all, but the signal itself has a frequency that matches the beats on the bottom figure.