We have examined the two-stage linear method of missing-data restoration, which calls for solving for a filter, interlacing it, and then solving for the missing data. I believe that method, with its interlacing, is unsuitable for data with a narrow spectral signal-to-noise ratio, such as we often encounter in practice. It would indeed be nice to be able to work with such data.
Recall equation (4):
![]()
Another possibility is that P0 should be the solution as found by the interlacing method. Time did not allow me to investigate this promising idea.
Still another possibility is that these problems are so easy to solve (requiring workstation compute times of a few seconds only) that we should abandon traditional optimization methods and use simulated annealing (Rothman, 1985).
All the above ideas are hopeful. A goal of this study is to define and characterize the kinds of problems that we think should be solvable. A simple example of a dataset that I believe should be amenable to interpolation, even with substantial noise, is shown in Figure 22. I have not worked with this case yet.
|
alias
Figure 22 Narrow-banded data that skilled humans can readily interpolate. | 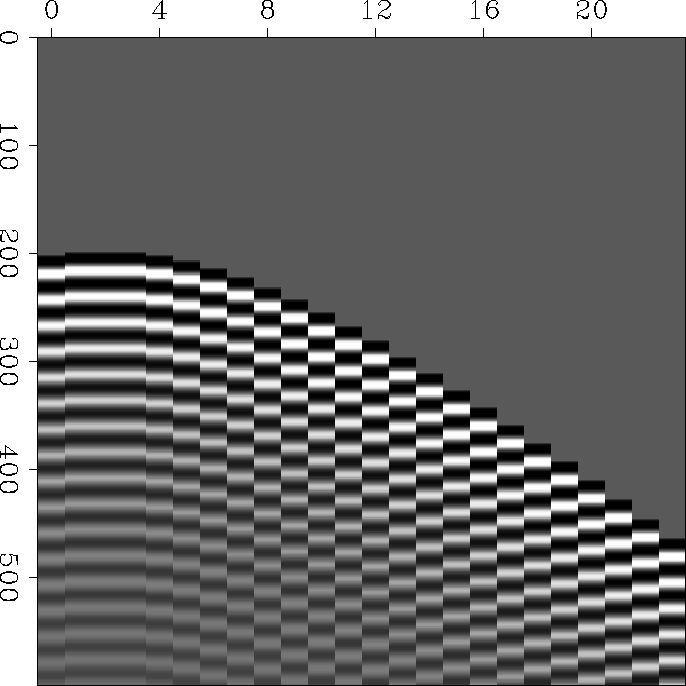 |
To prepare the way,
and to perform my preliminary (but unsatisfactory) tests,
I prepared subroutine hope(),
the two-dimensional counterpart to
missif() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
misfip()
and
misfip() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
subroutine hope( gap, h1,h2,hh, t1,t2,tt, a1,a2,aa, p1,p2,pp, known, niter)
integer h1,h2,h12, t1,t2,t12, a1,a2,a12, p1,p2,p12
integer i, gap, iter, niter, midpt, nx,nr, px,ax, qr,tr,hr
real hh(h1,h2), tt(t1,t2), aa(a1,a2), pp(p1*p2), known(p1*p2), dot
temporary real x( p1*p2 +a1*a2), rr( p1*p2 +p1*p2 +t1*t2)
temporary real g( p1*p2 +a1*a2), gg( p1*p2 +p1*p2 +t1*t2)
temporary real s( p1*p2 +a1*a2), ss( p1*p2 +p1*p2 +t1*t2)
p12 = p1*p2; a12 = a1*a2; t12 = t1*t2; h12= h1*h2;
nx = p12 + a12; px= 1; ax= 1+p12
nr = p12 + p12 + t12; qr= 1; hr= 1+p12; tr= 1+p12+p12
call zero( a12, aa); midpt= a1/2; aa( midpt, 1 ) = sqrt( dot( p12,pp,pp))
call zero( nx, x); call zero( nr, rr); call copy( p12, pp, x(px))
call zero( nx, g); call zero( nr, gg); call copy( a12, aa, x(ax))
do iter= 0, niter {
call cinloi( 0, 0, midpt,1, a1,a2,aa, p1,p2,pp, rr(qr))
call cinloi( 0, 0, midpt,1, h1,h2,hh, p1,p2,pp, rr(hr))
call cinloi( 0, 0, midpt,1, a1,a2,aa, t1,t2,tt, rr(tr))
call scaleit ( -1., nr, rr )
call cinloi( 1, 0, midpt,1, a1,a2,aa, p1,p2,g(px), rr(qr))
call cinlof( 1, 0, midpt,1, p1,p2,pp, a1,a2,g(ax), rr(qr))
call cinloi( 1, 1, midpt,1, h1,h2,hh, p1,p2,g(px), rr(hr))
call cinlof( 1, 1, midpt,1, t1,t2,tt, a1,a2,g(ax), rr(tr))
do i= 1, p12 { if( known(i) != 0.) g( i + (px-1)) = 0.}
do i= 1, midpt+gap { g( i + (ax-1)) = 0.}
call cinloi( 0, 0, midpt,1, a1,a2,aa, p1,p2,g(px), gg(qr))
call cinlof( 0, 1, midpt,1, p1,p2,pp, a1,a2,g(ax), gg(qr))
call cinloi( 0, 0, midpt,1, h1,h2,hh, p1,p2,g(px), gg(hr))
call cinlof( 0, 0, midpt,1, t1,t2,tt, a1,a2,g(ax), gg(tr))
call cgstep( iter, nx, x, g, s, _
nr, rr,gg,ss )
call copy( p12, x(px), pp)
call copy( a12, x(ax), aa)
}
return; end
I found the jump-and-interlace 2-D convolution cinjof() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) unsuitable here because it does not align its output consistently
with the aligning convolution cinloi()
unsuitable here because it does not align its output consistently
with the aligning convolution cinloi() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
So I wrote an aligning convolution identical with
cinloi() except that the filter is the adjoint.
It is called cinlof().
.
So I wrote an aligning convolution identical with
cinloi() except that the filter is the adjoint.
It is called cinlof().
# CINLOF -- Convolution INternal with Lags. Output is adjoint to FILTER.
#
subroutine cinlof( adj, add, lag1,lag2, n1,n2,xx, nb1,nb2,bb, yy)
integer adj, add, lag1,lag2, n1,n2, nb1,nb2
real xx(n1,n2), bb(nb1,nb2), yy(n1,n2)
integer y1,y2, x1,x2, b1, b2
call adjnull( adj, add, bb,nb1*nb2, yy,n1*n2)
if( adj == 0 )
do b2=1,nb2 { do y2= 1+nb2-lag2, n2-lag2+1 { x2= y2 - b2 + lag2
do b1=1,nb1 { do y1= 1+nb1-lag1, n1-lag1+1 { x1= y1 - b1 + lag1
yy(y1,y2) = yy(y1,y2) + bb(b1,b2) * xx(x1,x2)
}} }}
else
do b2=1,nb2 { do y2= 1+nb2-lag2, n2-lag2+1 { x2= y2 - b2 + lag2
do b1=1,nb1 { do y1= 1+nb1-lag1, n1-lag1+1 { x1= y1 - b1 + lag1
bb(b1,b2) = bb(b1,b2) + yy(y1,y2) * xx(x1,x2)
}} }}
return; end