




Next: References
Up: Discrete Fourier transform
Previous: Examples of 2-D FT
A basic building block in the
fast Fourier transform is called
``doubling.''
Given a series 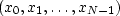 and its sampled Fourier transform
and its sampled Fourier transform 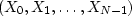 ,and another series
,and another series 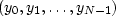 and its sampled Fourier transform
and its sampled Fourier transform 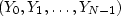 ,there is a trick to find easily
the transform of the interlaced double-length series
,there is a trick to find easily
the transform of the interlaced double-length series
| 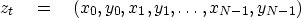 |
(20) |
The process of doubling is used many times
during the computing of a fast Fourier transform.
As the word ``doubling" might suggest,
it will be convenient to suppose that
N is an integer formed by raising 2 to
some integer power.
Suppose N = 8 = 23.
We begin by dividing our eight-point series
into eight separate series, each of length one.
The Fourier transform of each of the one-point series is just the point.
Next, we use doubling four times
to get the transforms of the four different two-point series
(x0, x4), (x1, x5), (x2, x6), and (x3, x7).
We use doubling twice more to get the transforms
of the two different four-point series
(x0, x2, x4, x6) and (x1, x3, x5, x7).
Finally, we use doubling once more
to get the transform of the original eight-point series
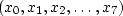 .It remains to look into the details of the doubling process.
Let
.It remains to look into the details of the doubling process.
Let
| 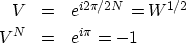 |
(21) |
| (22) |
By definition, the transforms of two N-point series are
| 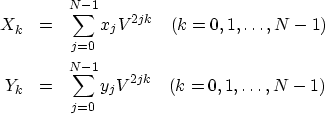 |
(23) |
| (24) |
Likewise, the transform of the interlaced series
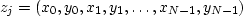 is
is
| 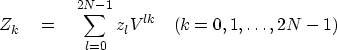 |
(25) |
To make Zk from Xk and Yk, we require two separate formulas,
one for k = 0, 1, 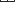 , N -1,
and the other for k = N, N + 1,
, N -1,
and the other for k = N, N + 1,
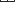 , 2N - 1.
Start from the sum
, 2N - 1.
Start from the sum
| 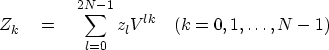 |
(26) |
and then split the sum into two parts,
noting that xj multiplies even powers of V,
and yj multiplies odd powers:
| 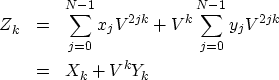 |
(27) |
| (28) |
We obtain the last half of the Zk by
| 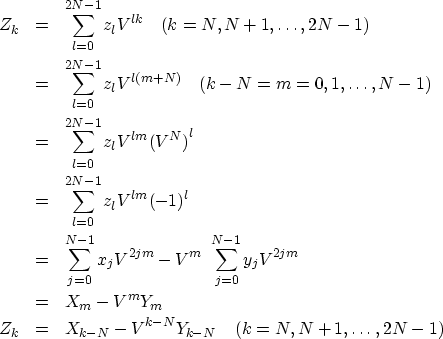 |
(29) |
| (30) |
| (31) |
| (32) |
| (33) |
| (34) |
| (35) |
The subroutine ftu() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) does not follow this analysis in detail.
does not follow this analysis in detail.
If you would like some industrial grade FFT programs,
search the web for "prime factor FFT".





Next: References
Up: Discrete Fourier transform
Previous: Examples of 2-D FT
Stanford Exploration Project
10/21/1998
![]() .It remains to look into the details of the doubling process.
Let
.It remains to look into the details of the doubling process.
Let
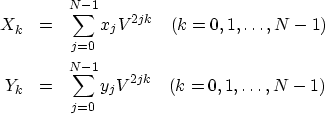
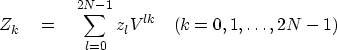
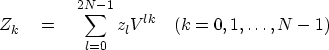
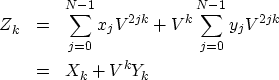
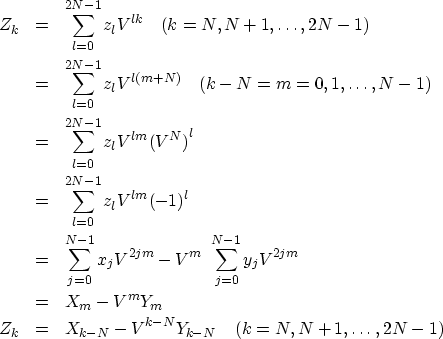
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) does not follow this analysis in detail.
does not follow this analysis in detail.