A particularly interesting factor is (1-Z), because the filter
(1,-1) is like a time derivative.
The time-derivative filter destroys
zero frequency
in the input signal.
The zero frequency is ![]() with a Z-transform
with a Z-transform ![]() .To see that the filter (1-Z) destroys zero frequency,
notice that
.To see that the filter (1-Z) destroys zero frequency,
notice that ![]() .More formally,
consider output Y(Z)=(1-Z)X(Z) made from the filter (1-Z)
and any input X(Z).
Since (1-Z) vanishes at Z=1,
then likewise Y(Z) must vanish at Z=1.
Vanishing at Z=1 is vanishing at frequency
.More formally,
consider output Y(Z)=(1-Z)X(Z) made from the filter (1-Z)
and any input X(Z).
Since (1-Z) vanishes at Z=1,
then likewise Y(Z) must vanish at Z=1.
Vanishing at Z=1 is vanishing at frequency ![]() because
because ![]() from (20).
Now we can recognize that multiplication of two functions of Z
or of
from (20).
Now we can recognize that multiplication of two functions of Z
or of ![]() is the equivalent of convolving the associated
time functions.
is the equivalent of convolving the associated
time functions.
| Multiplication in the frequency domain is convolution in the time domain. |
A popular mathematical abbreviation for the convolution operator is
an asterisk:
equation (9), for example,
could be denoted by
![]() .I do not disagree with asterisk notation,
but I prefer the equivalent expression Y(Z)=X(Z)B(Z),
which simultaneously exhibits
the time domain and the frequency domain.
.I do not disagree with asterisk notation,
but I prefer the equivalent expression Y(Z)=X(Z)B(Z),
which simultaneously exhibits
the time domain and the frequency domain.
The filter (1-Z) is often called a ``differentiator.'' It is displayed in Figure 7.
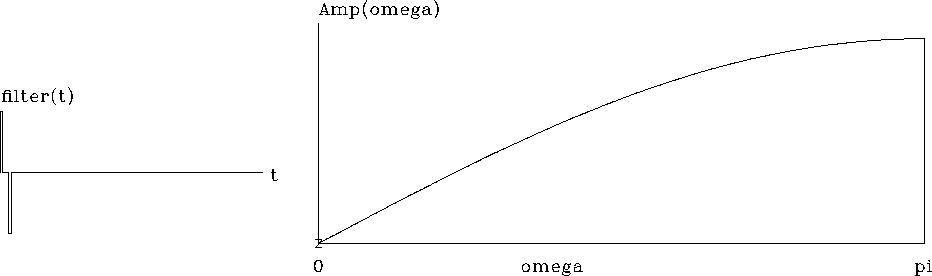 |
The letter ``z'' plotted at the origin
in Figure 7
denotes the root
of 1-Z at Z=1, where ![]() .Another interesting filter is 1+Z, which destroys
the highest possible frequency
.Another interesting filter is 1+Z, which destroys
the highest possible frequency ![]() ,where
,where ![]() .
.
A root is a numerical value for which a polynomial vanishes.
For example, ![]() vanishes
whenever Z=-2 or Z=1.
Such a root is also called a ``zero.''
The fundamental theorem of algebra says that if the highest
power of Z in a polynomial is ZN, then the polynomial
has exactly N roots,
not necessarily distinct.
As N gets large, finding these roots requires
a sophisticated computer program.
Another complication is that complex numbers can arise.
We will soon see that complex roots are exactly what we need
to design filters that destroy any frequency.
vanishes
whenever Z=-2 or Z=1.
Such a root is also called a ``zero.''
The fundamental theorem of algebra says that if the highest
power of Z in a polynomial is ZN, then the polynomial
has exactly N roots,
not necessarily distinct.
As N gets large, finding these roots requires
a sophisticated computer program.
Another complication is that complex numbers can arise.
We will soon see that complex roots are exactly what we need
to design filters that destroy any frequency.