




Next: Unitary and pseudounitary transformation
Up: UNITARY OPERATORS
Previous: UNITARY OPERATORS
A matrix operation like
 arises whenever we travel from one space to another and back again.
The inverse of this matrix arises when we ask to return from the other
space with no approximations.
In general,
arises whenever we travel from one space to another and back again.
The inverse of this matrix arises when we ask to return from the other
space with no approximations.
In general,  can be complicated beyond comprehension,
but we have seen some recurring features.
In some cases this matrix turned out to be a diagonal matrix
which is a scaling function in the physical domain.
With banded matrices, the
can be complicated beyond comprehension,
but we have seen some recurring features.
In some cases this matrix turned out to be a diagonal matrix
which is a scaling function in the physical domain.
With banded matrices, the
 matrix is also a banded matrix,
being tridiagonal for
matrix is also a banded matrix,
being tridiagonal for 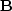 operators of both
(22)
and (21).
The banded matrix for the derivative operator (22)
can be thought of as the frequency domain weighting factor
operators of both
(22)
and (21).
The banded matrix for the derivative operator (22)
can be thought of as the frequency domain weighting factor  .We did not examine
.We did not examine  for the filter operator,
but if you do,
you will see that the rows (and the columns) of
for the filter operator,
but if you do,
you will see that the rows (and the columns) of  are the
autocorrelation
of the filter.
A filter in the time domain is simply a weighting function
in the frequency domain.
are the
autocorrelation
of the filter.
A filter in the time domain is simply a weighting function
in the frequency domain.
The tridiagonal banded matrix for linearly-interpolated NMO
is somewhat more complicated to understand,
but it somehow represents
the smoothing inherent to the composite process of NMO
followed by adjoint NMO,
so although we may not fully understand it,
we can think of it as some multiplication in the spectral domain
as well as some rescaling in the physical domain.
Since
 clusters on the main diagonal,
it never has a ``time-shift'' behavior.
clusters on the main diagonal,
it never has a ``time-shift'' behavior.





Next: Unitary and pseudounitary transformation
Up: UNITARY OPERATORS
Previous: UNITARY OPERATORS
Stanford Exploration Project
10/21/1998
![]() clusters on the main diagonal,
it never has a ``time-shift'' behavior.
clusters on the main diagonal,
it never has a ``time-shift'' behavior.