




Next: Pseudoinverse to nearest-neighbor NMO
Up: NORMAL MOVEOUT AND OTHER
Previous: Nearest-neighbor NMO
Typically, many receivers record every shot.
Each seismogram can be transformed by NMO
and the results all added.
This is called ``stacking'' or ``NMO stacking.''
The adjoint to this operation is to begin from
a model that is identical to the near-offset trace
and spray this trace to all offsets.
There is no ``official'' definition
of which operator of an operator pair is the operator itself
and which is the adjoint.
On the one hand, I like to think of the modeling operation itself
as the operator.
On the other hand,
the industry machinery keeps churning away at many processes
that have well-known names,
so I often think of one of them as the operator.
Industrial data-processing operators are typically adjoints
to modeling operators.
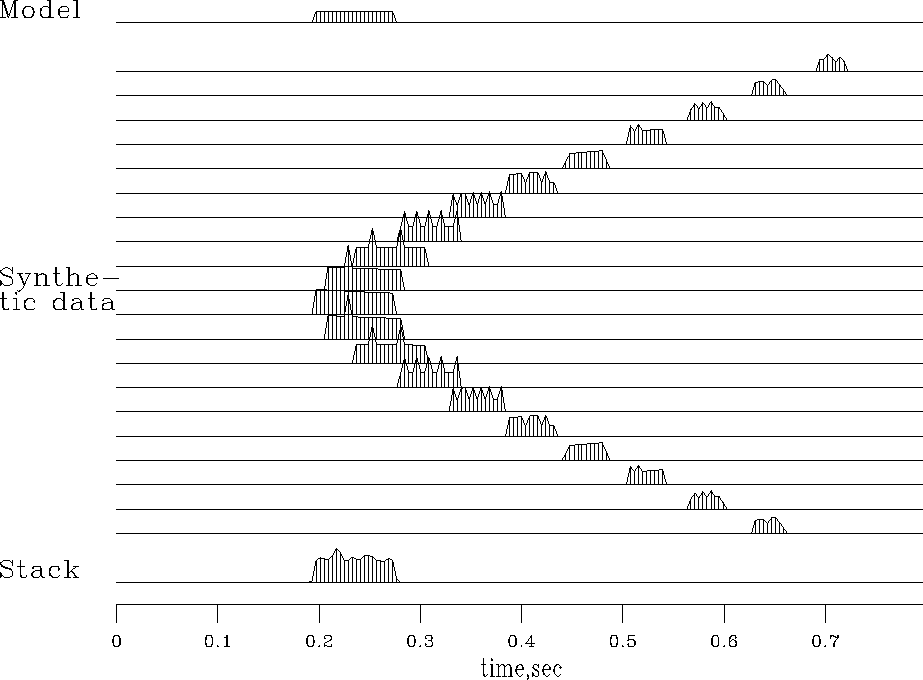
Figure 6 illustrates the operator pair, consisting
of spraying out a zero-offset trace (the model) to all offsets
and the adjoint of the spraying,
which is stacking.
The moveout and stack operations are in subroutine stack1().
subroutine stack1( adj, add, slow, t0,dt, x0,dx, nt,nx, stack, gather)
integer ix, adj, add, nt,nx
real x, slow(nt), t0,dt, x0,dx, stack(nt), gather(nt,nx)
call adjnull( adj, add, stack,nt, gather,nt*nx)
do ix= 1, nx {
x = x0 + dx * (ix-1)
call nmo1( adj, 1, slow, x, t0,dt, nt, stack, gather(1,ix))
}
return; end
Let  denote NMO, and let the stack be
defined by invoking stack1() with the conj=0 argument.
Then
denote NMO, and let the stack be
defined by invoking stack1() with the conj=0 argument.
Then  is the modeling operation
defined by invoking stack1() with the conj=1 argument.
Figure 6 illustrates both.
is the modeling operation
defined by invoking stack1() with the conj=1 argument.
Figure 6 illustrates both.





Notice the roughness on the waveforms caused by
different numbers of points landing in one place.
Notice also the increase of AVO
as the waveform gets compressed into a smaller space.
Finally, notice that the stack is a little rough,
but the energy is all in the desired time window.
We notice a contradiction of aspirations.
On the one hand,
an operator has smooth outputs if it
``loops over output space''
and finds its input where-ever it may.
On the other hand,
it is nice to have modeling and processing
be exact adjoints of each other.
Unfortunately,
we cannot have both.
If you loop over the output space of an operator,
then the adjoint operator has a loop over input space
and a consequent roughness of its output.
Unfortunately,
the adjoint operator  defined by the subroutine nmo1()
defined by the subroutine nmo1() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is not a good operator for seismogram modeling--notice
the roughness of the synthetic seismograms
in Figure 6.
This roughness is not an inevitable consequence
of nearest-neighbor interpolation.
It is a consequence of defining the NMO program as a loop
over the output space
is not a good operator for seismogram modeling--notice
the roughness of the synthetic seismograms
in Figure 6.
This roughness is not an inevitable consequence
of nearest-neighbor interpolation.
It is a consequence of defining the NMO program as a loop
over the output space  .Instead,
we can define inverse NMO
as a loop over its output space,
which is not
.Instead,
we can define inverse NMO
as a loop over its output space,
which is not  but t.
This is done in imo1()
but t.
This is done in imo1() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
subroutine imo1( adj, add, xs, t0, dt, nt, zz, tt )
integer adj, add, nt, it, iz
real t0, dt, zz(nt), tt(nt), t, xs, zsquared
call adjnull( adj, add, zz,nt, tt,nt)
do it= 1, nt { t = t0 + dt*(it-1)
zsquared = t * t - xs * xs
if ( zsquared >= 0.) { iz = 1.5 + (sqrt( zsquared) - t0) /dt
if ( iz > 0 ) { if( adj == 0 )
tt(it) = tt(it) + zz(iz)
else
zz(iz) = zz(iz) + tt(it)
}
}
}
return; end
# inverse moveout and spray into a gather.
#
subroutine imospray( adj, add, slow, x0,dx, t0,dt, nx,nt, stack, gather)
integer ix, adj, add, nx,nt
real xs, slow, x0,dx, t0,dt, stack(nt), gather( nt,nx)
call adjnull( adj, add, stack,nt, gather, nt*nx)
do ix= 1, nx {
xs = (x0 + dx * (ix-1)) * slow
call imo1( adj, 1, xs, t0, dt, nt, stack, gather(1,ix))
}
return; end





Next: Pseudoinverse to nearest-neighbor NMO
Up: NORMAL MOVEOUT AND OTHER
Previous: Nearest-neighbor NMO
Stanford Exploration Project
10/21/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif)