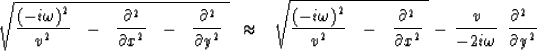Next: Separability of 3-d migration
Up: SPLITTING AND FULL SEPARATION
Previous: Application to lateral velocity
The operator for migration of zero-offset
reflection seismic data in three
dimensions is expandable to second
order by Taylor series expansion
to the so-called 15 approximation
approximation
| 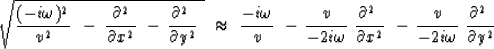 |
(5) |
The most common case is when v is slowly variable
or independent of x and y.
Then the conditions of full separation do apply.
This is good news because it means that we
can use ordinary 2-D wave-extrapolation
programs for 3-D, doing the in-line
data and the out-of-line data in either order.
The bad news comes when we try for more accuracy.
Keeping more terms in the Taylor series
expansion soon brings in the cross
term 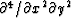 .Such a term allows neither full separation nor splitting.
Fortunately, present-day marine data-acquisition techniques
are sufficiently crude in the out-of-line
direction that there is little
justification for out-of-line
processing beyond the 15
.Such a term allows neither full separation nor splitting.
Fortunately, present-day marine data-acquisition techniques
are sufficiently crude in the out-of-line
direction that there is little
justification for out-of-line
processing beyond the 15 equation.
Francis Muir had the good idea of representing
the square root as
equation.
Francis Muir had the good idea of representing
the square root as
| 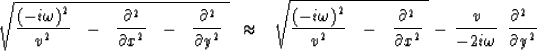 |
(6) |
There may be justification for better approximations with land data.
Fourier transformation of at least one
of the two space axes will solve the computational problem.
This should be a good approach
when the medium velocity does not vary
laterally so rapidly as to invalidate application
of Fourier transformation.





Next: Separability of 3-d migration
Up: SPLITTING AND FULL SEPARATION
Previous: Application to lateral velocity
Stanford Exploration Project
10/31/1997
![]() approximation
approximation