Recursive-dip-filter implementation

Implementation of the moderate bandwidth dip filters is, again, a straightforward matter. For example, clearing fractions, the low-pass filter becomes  

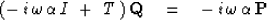$$( -\, i\, \omega \, \alpha\, I\ +\ T\,)\, {\bf Q} \eq -\, i\, \omega \, \alpha\, {\bf P}$$ (22)

The main trick is to realize that the differentiation implied by 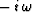$- \,i\, \omega$ is performed in a Crank-Nicolson sense. That is, terms not differentiated are averaged over adjacent values.  

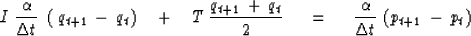$$I\ {\alpha \over \Delta t}\ \left( \,q_{t+1} \,-\, q_t \righ... ...ver 2 }\ \eq \ {\alpha \over \Delta t} \ ( p_{t+1} \,-\, p_t )$$ (23)

Gathering the unknowns to the left gives  

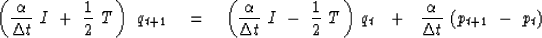$$\left( {\alpha \over \Delta t}\ I\ +\ {1 \over 2 }\ T\, \rig... ...)\, q_t \ \ +\ \ {\alpha \over \Delta t}\ ( p_{t+1} \ -\ p_t )$$ (24)

Equation (24) is a tridiagonal system of simultaneous equations for the unknowns q _{t + 1}. The system may be solved recursively for successive values of t.

The parameter $\alpha$ determines the filter cutoff. It can be chosen to be any function of time and space. However, if the function is to vary extremely rapidly, then it may be necessary to incorporate some of the stability analysis that is developed in a later chapter for use with wave equations.