Schneider [1978] states the analytic representation for the Huygens secondary wavelet
| |
(19) |
Equation (19) states the two -dimensional Huygens wavelet, not the three -dimensional wavelet (which differs in some minor aspects). Although waves from point sources are mainly spherical, the focusing of bent layers is mainly a two-dimensional focusing, i.e., bent layers are more like cylinders than spheres.
You might wonder why anyone would prefer approximations,
given the exact inverse transform (19).
The difficulty of graphing (19) shows up in practice as a difficulty
in convolving it with data.
That is why early Kirchhoff migrations were generally recognizable
by precursor noise above a flat sea floor.
Chapters ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , and
, and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
are largely devoted to extensions of (19) that
are valid with variable velocity and that are better representations
on a data mesh.
,
are largely devoted to extensions of (19) that
are valid with variable velocity and that are better representations
on a data mesh.
In the Fourier domain, the Huygens secondary source function
is simple and smooth.
It is a straightforward matter to evaluate the function on a rectangular mesh
and inverse transform with ft1axis() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and ft2axis()
and ft2axis() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
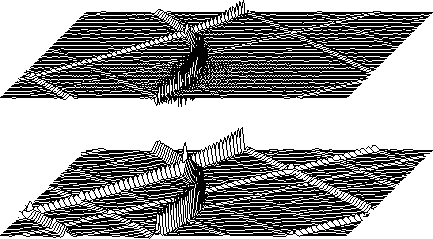
Figure 8
shows the result on a 256
.
Figure 8
shows the result on a 256 ![]() 64 point mesh.
64 point mesh.
 |
(In practice the mesh would be about 1024 ![]() 256 or more,
but the coarser mesh used here provides a plot of suitable detail).
Because of the difficulty in plotting functions that resemble
an impulsive doublet, a second plot of the time integral,
(with gentle band limiting)
is displayed in the lower part of Figure 8.
256 or more,
but the coarser mesh used here provides a plot of suitable detail).
Because of the difficulty in plotting functions that resemble
an impulsive doublet, a second plot of the time integral,
(with gentle band limiting)
is displayed in the lower part of Figure 8.