




Next: The substitution operator
Up: COSMETIC ASPECT OF WAVE
Previous: Spatial scaling before migration
Exponential scaling functions have some ideal mathematical properties.
Take the Z-transform of a time function at:
|  |
(9) |
The exponentially gained time function is defined by
|  |
(10) |
The symbol  denotes exponential gain.
Mathematically,
denotes exponential gain.
Mathematically,  means that Z is replaced by
means that Z is replaced by 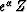 .Polynomial multiplication amounts to convolution of the coefficients:
.Polynomial multiplication amounts to convolution of the coefficients:
| 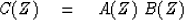 |
(11) |
By direct substitution,
| 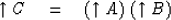 |
(12) |
This means that exponential gain can be done either before or after convolution.
You may recall from
Fourier transform theory that multiplication of a time function
by a decaying exponential 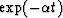 is the equivalent
of replacing
is the equivalent
of replacing 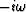 by
by 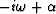 in the transform domain.
in the transform domain.
Specialize the downward-continuation operator 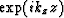 to
some fixed z and some fixed kx.
The operator has become a function of
to
some fixed z and some fixed kx.
The operator has become a function of 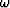 that may be expressed
in the time domain as a filter at.
Hyperbola flanks move
upward
on migration.
So the filter is
anticausal.
This is denoted by
that may be expressed
in the time domain as a filter at.
Hyperbola flanks move
upward
on migration.
So the filter is
anticausal.
This is denoted by
|  |
(13) |
The large negative powers of Z are associated with the hyperbola flanks.
Exponentially boosting the coefficients of positive powers of Z
is associated with diminishing negative powers--so
 is A with a weakened tail--and
tends to attenuate flanks rather than move them.
Thus
is A with a weakened tail--and
tends to attenuate flanks rather than move them.
Thus  may be described as viscous.
may be described as viscous.
From a purely physical point of view cosmetic functions like gain
control and dip filtering should be done after processing, say,  .But
.But 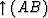 is equivalent to (
is equivalent to (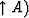 (
(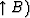 ,and the latter operation amounts to using a viscous operator
on exponentially gained data.
In practice, it is common to
forget the viscosity and create A(
,and the latter operation amounts to using a viscous operator
on exponentially gained data.
In practice, it is common to
forget the viscosity and create A(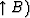 .Perhaps this means that dipping events carry more information than flat ones.
.Perhaps this means that dipping events carry more information than flat ones.





Next: The substitution operator
Up: COSMETIC ASPECT OF WAVE
Previous: Spatial scaling before migration
Stanford Exploration Project
10/31/1997
![]() to
some fixed z and some fixed kx.
The operator has become a function of
to
some fixed z and some fixed kx.
The operator has become a function of ![]() that may be expressed
in the time domain as a filter at.
Hyperbola flanks move
upward
on migration.
So the filter is
anticausal.
This is denoted by
that may be expressed
in the time domain as a filter at.
Hyperbola flanks move
upward
on migration.
So the filter is
anticausal.
This is denoted by
![]() .But
.But ![]() is equivalent to (
is equivalent to (![]() (
(![]() ,and the latter operation amounts to using a viscous operator
on exponentially gained data.
In practice, it is common to
forget the viscosity and create A(
,and the latter operation amounts to using a viscous operator
on exponentially gained data.
In practice, it is common to
forget the viscosity and create A(![]() .Perhaps this means that dipping events carry more information than flat ones.
.Perhaps this means that dipping events carry more information than flat ones.